Poglavje 8 Protokoli
V Cambridgeovem slovarju lahko najdemo naslednje (nekoliko) različne opredelitve protokola (“Protocol” 2018):
- V politiki *: formalni mednarodni sporazum med vladami o določeni dejavnosti.
Trgovinske odnose med nedavnimi članicami Evropske unije ureja strog protokol, ti. kjotski protokol
- V IT *: Nabor tehničnih pravil, ki nadzorujejo izmenjavo informacij med različnimi računalniki ali računalniška omrežja (stranke).
- V sociologiji *: Sistem pravil in sprejemljivega vedenja, ki bi se ga morali držati ljudje ali organizacije v uradnih situacijah, na primer, ko imajo uradne razprave: po incidentu prejšnji teden so uradniki zadolženi za varnost letališč dobili navodila za pregled varnostnih predpisov in protokola.
Protokoli v kriptografiji sledijo definiciji IT. Poleg tega si kriptografski protokol ** prizadeva ** ne razkriti več (npr. s pomočjo podatkov), kot je določeno v protokolu.
8.1 Protokoli v vsakdanjem življenju
Vsakodnevno življenje je polno protokolov. Uporabljamo jih lahko za določitev, kako se obnašati, kako delati, kako jesti, kako nadaljevati poskus …
Opazujmo nekatere izmed njih.
Prvi je bolj povezan z užitkom, naravo, sprostitvijo, SKALAMI!
- Plezalni signali
Iz hribov: Svoboda hribov
“Učinkovita komunikacija med plezalcem in njegovim usmerjevalcem je bistvenega pomena za varnost in učinkovitost. Plezalci so z leti razvili nabor splošno sprejetih vrvnih signalov, vsakega z drugačnim zvokom, tako da je mogoče tudi pravilno razlagati besede, ki jih raznaša veter.”
Slika 8.1: plezalni protokol
- Družbeni bonton srečanja
Pozdravljanje in rokovanje plemstva v Franciji.
Na svojih potovanjih boste naokrog po svetu naleteli na veliko plemičev. Določene so tradicije, kako ravnati, ko naletite na plemiče ali celo na določene lokacije. Sledi nekaj smernic za etiketo srečevanja ljudi.
DEJANJA PRIJAZNOSTI Sledijo pravilni načini izvedbe pozdravljanja.
PRIKLON Običajno je, da se gospod prikloni. Na splošno je bolje, da se gospod med priklanjanjem upogne ob odpadke in spusti zgornji del telesa. V primeru da nosi klobuk, ga mora me priklanjanjem sneti. V večini situacij mora med priklanjanjem tudi prikimati.
PRIKLON #2 Običajno je, da se dama prikloni. Na splošno je bolje, da dama med priklanjanjem gre na kolena in spusti celotno telo. Dama si mora pridržati krilo, da le-to ne pade na tla. Hrbet mora imeti izravnan kolikor je le-to mogoče. V večini situacij mora med priklanjanjem tudi prikimati.
KLEČANJE Gospod na koncu priklona poklekne na desno nogo. Tudi dama na koncu priklona poklekne in sicer z obema kolenoma dokler se ne dotakne tal. Dami ni potrebno poklekniti do tal zunaj, predvsem če razmere niso primerna (Čeprav bi gospod poskrbel za primerno podlago za damo). Med poklekanjem mora vsak posameznik premakniti glavo naprej in ne sme gledati višje od kolen osebe pred katero pokleka.
ROKOVANJE Gospod bo vzel ponujeno roko drugega gospoda in jo čvrsto stisnil, ne drobeč, in to le enkrat. Gospod bo vzel ponujeno roko dame in jo nežno položil v svojo in jo narahlo stisnil ali poljubil na njene členke. Gospod nikoli ne ponudi svoje roke dami, dama mora prva ponuditi, iztegujoč roko, zapestje narahlo upognjeno in z dlanjo obrnjeno navzdol.
POLJUB Dva posameznika, ki sta si blizu, ne glede na spol, si bosta lahko, ko se srečata in objameta v javnosti, izmenjala poljub na levem licu ali pa kar na obeh. Edino v času poroke in ostalih praznovanj je primerno da se dva poljubita v javnosti. Vsa druga izkazovanja naklonjenosti v javnosti niso dobrodošla ali sprejemljiva.
- THE SALUTE A military salute is performed by either sex by bringing the right arm up until it is parallel with the ground and bent so that the tips of the fingers, held ridged, just touch above the right eye. The palm of the hand should be facing directly outwards, not inward. If a soldier is carrying a pole-arm or rifle the salute should be delivered across the chest to the left shoulder, instead of the forehead. Traditionally, a soldier should stand at attention when saluting.
Vojaški pozdrav opravlja vojak/inja tako, da desno roko dvigne navzgor, dokler ni vzporedna s tlemi in se upogne tako, da se konice prstov, oprijete, samo dotaknejo nad desnim očesom. Dlan mora biti obrnjena navzven, ne navznoter. Če ima vojak palico ali puško, je treba odzdraviti preko prsnega koša na levo ramo, namesto čelo. Tradicionalno bi moral biti vsak vojak pozoren pri pozdravljanju.
8.2 Protokoli v kriptografiji
V kriptografiji si dve osebi želita izmenjati sporočilo (imenujmo ju Ana in Bor). Njun cilj je, da lahko sporočilo prebereta le ona dva, zato se morata dogovoriti, kako bosta sporočilo šifrirala. Temu dogovoru oz. pravilom pravimo protokol. Primer protokola v kriptografiji je one time pad, ki ga bomo tudi podrobneje spoznali.
8.2.1 One time pad (Bor)
One time pad deluje tako kot Vigenerjeva šifra, ampak da je ključ enako dolg kot besedilo. S tem dosežemo, da je vsaka črka sporočila zašifrirana s svojo črko ključa. Ponavadi zgeneriramo dolg ključ in za vsako poslano sporočilo uporabimo nov del ključa. Če se tega držimo in če ključa nima nihče drug, potem je komunikacija popolnoma varna, kar pomeni da iz kriptograma nihče ne more ugotoviti sporočila. Predstavljajmo si, da smo prestregli nek kriptogram. Dolžina sporočila in ključa sta enaki, zato imamo enako število različnih možnih ključev kot sporočil. Ker z vsakim ključem dobimo drugačno sporočilo, lahko kriptogram predstavlja vsako možno sporočilo. Po drugi strani pa je največja slabost, da je treba najprej izmenjati ključ, ki je enako dolg kot sporočilo, bi bilo lažje takoj izmenjati kar sporočilo.
Za prikaz delovanja protokola one time pad moraš najprej zgenerirati ključ. Nato napišeš sporočilo, ki ga želiš poslati in ga zašifriraš. Ob tem se del ključa odebeli, kar prikazuje kateri del ključa smo uporabili. Kriptogram potem pošlješ prejemniku, ki ga mora odšifrirati. Potem lahko na to sporočilo odgovori. Ko je ves ključ uporabljen, je potrebno zgenerirati novega.
8.2.2 Varnost protokola one time pad
V uvodu smo že omenjali varnost kriptosistemov.
Za analizo varnosti kriptosistema opazujemo moč napadalca na tem sistemu. Močnejši je napadalec, manj varen je kriptosistem. eCrpto Book
Chapter: Introduction.
Naj bo \(E=(E,D)\) Shanonnova šifra definirana nad \((K,M,C)\) in naj bo \(k\) slučajna spremenljivka nad \(K\) z enakomerno porazdelitvijo. Če za vsak \(m_0,m_1 \in M\) in za vsak \(c \in C\) velja \[ Pr[E(k,m_0)=c] = Pr[E(k,m_1)=c] \] potem \(E\) imenujemo popolno tajna Shanonnova šifra.
Shanonnova šifra je par funkcij \(E=(E,D)\), za kateri velja:
- Funkcija \(E\) (šifrirna funkcija) dobi kot parametre ključ \(k\) in sporočilo \(m\), njen rezultat je tajnopis \(c\). Torej \(c=E(k,m)\).
- Funkcija \(D\) (odšifrirna funkcija) dobi kot parametre ključ \(k\) in tajnopis \(c\), njej rezultat je sporočilo \(m\). Torej \(m=D(k,c)\).
- Za vsak ključ \(k\) in vsako sporočilo \(m\), mora veljati \(D(k,E(k,m))=m\).
Naj bo \(E=(E,D)\) šifra definirana nad \((K,M,C)\). Z \(A\) označimo prisluškovalca. Definirajmo dva poskusa, Poskus 0 in Poskus 1. Za \(b=0,1\) definiramo Poskus \(b\):
- Prisluškovalec izbere \(m_0, m_1 \in M\) iste dolžine in ju pošlje izzivalcu.
- Izzivalec ibere \(k \in K, c \in E(k, m_b)\) in pošlje \(c\) prisluškovalcu.
- Prisluškovalec vrne bit \(b' \in \{0, 1\}\). Za \(b=0,1\) naj bo \(W_b\) dogodek, da prisluškovalec \(A\) vrne 1 pri Poskusu \(b\).
Definirajmo semantično varnost (ang. semantic security advantage) glede na šifro \(E\) kot: \[ SSadv[A, E] := |Pr[W_0] - Pr[W_1]| \]
Šifra \(E\) je semantično varna, če je za vsakega prisluškovalca A vrednost \(SSadv[A, E]\) zanemarljivo majhna.
Če zahtevamo le semantično varnost, lahko One Time Pad malo poenostavimo. Namesto, da generiramo dolg ključ, lahko uporabimo ključ dolžine \(\ell\) in ga razširimo na dolžino sporočila. Če je razširitev deterministična (tj. za isti vhodni ključ vedno dobimo isti razširjen ključ), potem smo One Time Pad spremenili v tokovno šifro (ang. Stream cipher). V 4. poglavju smo že predstavili nekaj tokovnih šifer.
Čeprav je OTP semantično varen, ne zazna, če je bil kriptogram spremenjen med pošiljanjem. Prisluškovalec med pošiljateljem in prejemnikom lahko kriptogram poljubno spremeni in tako spremeni sporočilo, ki ga bo prejemnik dobil.
Predpostavimo, da napadalec dobi kriptogram \(c = m \oplus k\) in ga spremeni v \(c' = c \oplus \Delta\). Potem prejemnik dobi sporočilo: \[ D(k, c') = k \oplus c \oplus \Delta = m \oplus \Delta \]
8.3 Protokoli za izmenjavo ključev
V uvodu smo govorili o simetrični in asimetrični kriptografiji. Spomnite se primerov, ko Ana in Bob uporabljata skupno deljeno skrivnost, ki je vsem drugim neznana. Ali smo že kaj povedali o tem, kako sta si omislila skupni ključ? Ne. No, gre za protokole za izmenjavo ključev.
Protokoli izmenjave ključev (Key agreementna kratko KE)
so mehanizmi, s katerimi dve strani, ki komunicirata prek neprimerno nadzorovanega omrežja, lahko ustvarijo (izračunajo) skupni skrivni ključ.
Opazite, da je treba protokole za izmenjavo ključev opraviti na zelo pameten način. Poleg tega, kaj je dober protokol za izmenjavo ključev? Ali želimo samo, da bi dve stranki lahko izračunali skupno skrivnost ali kaj več?Mogoče potrditev, da sta to izračunali? Ali pa da jih lahko izračunata le oni? Vse dodatne skrbi lahko olajšajo ali otežijo problem izmenjave ključev.
Preverjeni protokol izmenjave ključev (na kratko AKE) dveh strank je mehanizem, ki omogoča:
- da dve stranki izračunata skupno skrivnost,
- da je dvema strankama omogočeno, da vesta, o kom govorita.
Z drugimi besedami, AKE protokol bi moral dvema uporabnikoma omogočiti vzpostavitev skupnega ključa, imenovanega ključ seje. Ob koncu uspešnega izvajanja takšnega protokola bi moral imeti uporabnik, recimo \(P\), jasno idejo, s katerim uporabnikom, recimo \(Q\), se pogovarja, torej s katerim uporabnikom je vzpostavil skupni uporabnik ključ seje (to je mogoče določiti pred zagonom protokola ali med izvedba protokola). Varni protokol AKE bi moral zagotoviti, da je ključ seje \(P\) učinkovit svež, naključen ključ, ki ga poznamo le \(Q\) [@ BonehShoup_0_4].
Authenticated Key-exchange protocol with confirmation (AKC in short) of two parties is an mechanisms that enables
- for two parties to compute the common secret,
- for two parties to enable make them know to who they are talking about,
- a confirmation computing the common secret key on and to both sides.
In other words, AKC protocol should allow two users all that AKE protocol enables, plus that say \(P\), should have a clear idea if the user \(Q\) has or has not calculated the common secret (the key).
8.4 Kako deliti skrivnosti
Danes že vsi vemo, da imajo informacije podobno, včasih celo večjo vrednost kot denar. Zato moramo biti pri dodeljevanju dostopa do njih skrajno previdni. Iz izkušenj vemo, da ni dobro povsem zaupati nobenemu posamezniku, še posebej, če je v njegovih rokah usoda mnogih. Vedno se tudi lahko zgodi, da je uporabnik neupravičeno izključen iz sistema (npr. če izgubi ključe) ali da nepooblaščeni uporabniki uspejo vdreti v sistem.
V prispevku bomo predstavili nekaj splošnih postopkov za deljenje skrivnosti. Le-ti sodijo med osnovne prijeme za povečanje zaupanja v delovanje informacijskih sistemov. To področje predstavlja enega izmed stebrov moderne kriptografije in je tesno povezano s skrbjo za varno in odgovorno ravnanje s ključi.
Za začetek si oglejmo nekaj zanimivih primerov deljenja skrivnosti.
Na tajnem projektu dela \(n\) oseb, materiali o projektu pa so spravljeni v trezorju z več ključavnicami. Dostop do materialov je dovoljen le tedaj, kadar se zbere večina, tj. več kot polovica oseb. Vsak sodelavec dobi enako število ključev. Koliko najmanj ključavnic je potrebno in koliko ključev mora dobiti vsak?
Predno si pogledaš rešitev, morda poskusi rešiti nalogo za \(n=2,3,4,\dots\), nato pa tvegaj z napovedjo, kaj bi utegnila biti dobra spodnja meja za število ključavnic.
Rešitev: Predpostavimo najprej, da nam je ključe uspelo razdeliti tako, kot zahteva naloga, in poglejmo kaj znamo ugotoviti o številu ključev. Naj bo \(k=\lfloor (n\!+\!1)/2\rfloor\) in \({s={n\choose k}}\). Potem obstaja natanko \(s\) različnih \(k\)-elementnih podmnožic oseb, ki delajo na tajnem projektu: \(G_1, G_2,\dots, G_s\). Vsaka skupina \(G_i\) vsebuje vsaj \((n/2)\) oseb, zato osebe zunaj te skupine nimajo vseh ključev. Naj bo \(K_i\) množica ključev, ki jim manjkajo. Potem nobena izmed množic \(K_i\) \((1\le i \le s)\), ni prazna. Skupaj s katerimkoli članom skupine \(G_i\) pa imajo vse ključe, torej ima vsaka oseba iz \(G_i\) vse ključe iz \(K_i\). Naj bo \(i\ne j\). V množici \(G_i\) obstaja oseba, ki ni v \(G_j\). Ta oseba nima nobenega izmed ključev iz \(K_j\), torej je \(K_i\cap K_j=\emptyset\). Ker sta bila \(i\) in \(j\) poljubna, od tod sledi, da je različnih ključev vsaj \(s\).
Sedaj pa pokažimo, da je \(s\) ključev \(k_1,\dots,k_s\), vedno tudi dovolj za rešitev zastavljene naloge. Ključe razdelimo tako, da dobijo ključ \(k_i\) natanko vse osebe iz skupine \(G_i\). Tako dobi vsaka oseba \({n-1 \choose k-1}\) ključev. Le večinska skupina ima neprazen presek z vsemi podmnožicami \(G_i\), tako da lahko le taka skupina odpre trezor.
Najprej smo ugotovili, da mora biti ključavnic vsaj \(s\), nato pa smo našli način, kako dodeliti vsaki osebi \({n-1\choose k-1}\) ključev, tako da bodo lahko le večinske skupine odklenile vse ključavnice.
V banki morajo trije direktorji vsak dan odpreti trezor, vendar pa kombinacije ne želijo zaupati nobenemu posamezniku. Zato bi radi imeli sistem, po katerem lahko odpreta trezor poljubna dva med njimi.
Zgornja rešitev nam svetuje (\(n=3\), \(k=2\), \(s={3 \choose 2}=3\)), da nastavimo na trezor tri ključavnice in damo vsakemu direktorju dva ključa (seveda pa nobenemu isti par). Vendar pa lahko v tem primeru vsak direktor odklene dve ključavnici in že s tem bistveno oslabi varnost, npr. za trikrat skrajša čas, potreben za odstranitev ključavnic.
Želimo najti rešitev, ki ne bo nikomur dala prednosti pred zunanjim vlomilcem. Ta problem lahko rešimo z \((2,3)\)-stopenjsko shemo za deljenje skrivnosti, glej sliko 1. Takšne sheme sta leta 1979 neodvisno odkrila Blakley in Shamir.
Slika 1
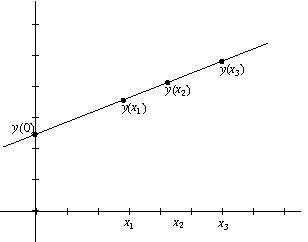
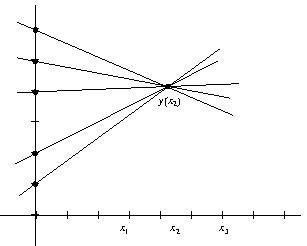
\((2,n)\)-stopenjska shema za deljenje skrivnosti, \(n\in \mathbb{N}\). Delivec si v ravnini izbere premico \(\ell\), ki ni navpična, in za vsako osebo na tej premici izbere svojo točko, ki ne leži na osi \(y\). Za zgornji sliki si izberemo \(n=3\).
Vsaka oseba dobi le koordinato \(y\) svoje točke, ki jo shrani na primer na pametni kartici. Program v trezorju pozna še ustrezne od 0 različne koordinate \(x\), zato lahko izračuna ključ \(y(0)\), ki je enak odseku, kjer premica \(\ell\) seka os \(y\). Vsaki dve točki natanko določata premico in s tem ključ.
Če imamo eno samo točko, ne moremo ugotoviti, kateri ključ je pravi, saj so vsi videti enako dobri.
V Rusiji so v 90-ih letih prejšnjega stoletja uporabljali \((2,3)\)-stopenjsko shemo za kontrolo jedrskega orožja (predsednik, obrambni minister, vrhovni vojaški poveljnik).
V splošnem je \((t,n)\)-stopenjska shema za deljenje skrivnosti \(K\) med \(n\) oseb, \(2\le t \le n\), metoda, za katero velja:
poljubnih \(t\) oseb lahko izračuna skrivnost \(K\),
nobena skupina s \(t-1\) (ali manj) osebami ne more izračunati prav nobene informacije o skrivnosti \(K\).
Sheme za deljenje skrivnosti so vsestransko uporabne. Lahko jih uporabimo povsod, kjer do podatkov dostopamo hierarhično. Tak način dostopa je pogost v velikih podjetjih, bankah in vojski.
Če računamo z običajnimi tipi števil, ki so na voljo v standardnih programskih jezikih, moramo rezultate izračunov zaradi omejene velikosti teh tipov nenehno zaokrožati (posebno ko postajajo števila vse večja in večja ali pa jih delimo). V kriptografiji pa približki ne zadoščajo, zato si za računanje raje omislimo končne množice kot pri številčnici na uri. Tak zgled so kolobarji \(\mathbb{Z}_n\), \(n\in \mathbb{N}\), v katerih računamo po modulu števila \(n\). Za elemente vzamemo \(\{0,1,\dots,n-1\}\), računamo pa tako, da seštejemo ali zmnožimo dve števili tako, da pravi rezultat nadomestimo z njegovim ostankom pri deljenju z modulom \(n\). Na primer za \(n=7\) velja \(4+5 \mod 7 =2\) in \(5\cdot 4 \mod 7 =6\), saj ima vsota 9 ostanek 2 pri deljenju s 7, produkt 20 pa ostanek 6.
Videli smo že, kako z geometrijskim argumentom zasnujemo \((2,n)\)-stopenjsko shemo za deljenje skrivnosti. Poglejmo sedaj, kako skonstruiramo \((t,t)\)-stopenjsko shemo za deljenje skrivnosti:
Naj bo \(m\) neko dovolj veliko naravno število (\(m \ge t+1\)), \(K\in \mathbb{Z}_m\) (skrivnost) in \({\cal P}=\{P_1,\dots,P_t\}\) množica oseb, ki jim želimo razdeliti skrivnost.
Delivec \(D\notin {\cal P}\) neodvisno izbere naključna števila \(y_1,y_2,\dots,y_{t-1} \in \mathbb{Z}_m\) in izračuna \[ y_t = K -(y_1+\cdots +y_{t-1}) \mod m. \]
Oseba \(P_i\) dobi del \(y_i\) \((1\le i \le t)\).
Osebe \(P_1,\dots,P_{i-1},P_{i+1},\dots,P_t\) lahko izračunajo samo \(K-y_i\), kar pa jim nič ne pomaga, saj je bilo število \(y_i\) naključno izbrano, medtem ko vsi skupaj samo seštejejo svoje dele in dobijo skrivnost \(K\).
Shamir je skonstruiral splošno \((t,n)\)-stopenjsko shemo za deljenje skrivnosti za poljubni naravni števili \(t\) in \(n\), \(2\le t \le n\). Za tako shemo je dovolj, da v \((2,n)\)-stopenjski shemi za deljenje skrivnosti nadomestimo premico s polinomom stopnje \(t\!-\!1\), saj je tak polinom določen s \(t\) točkami.
Spomnimo se, da je polinom spremenljivke \(x\) definiran s predpisom \[ f(x)=a_0+ a_1 x+\cdots + a_n x^n,\ \ \ \ \ \ \ a_i \in {\cal O}, \] kjer je \({\cal O}\) nek obseg (npr. \(\mathbb{R}\) ali pa \(\mathbb{Z}_p\), \(p\) praštevilo). Ničla polinoma \(f(x)\) je taka vrednost \(a\in {\cal O}\), za katero je \(f(a)=0\).
V praštevilskih kolobarjih \(\mathbb{Z}_p\), kjer je \(p\) praštevilo, je možno tudi deljenje z vsakim od 0 različnim elementom \(a\in \mathbb{Z}_p\) in zato tudi sodijo med obsege. Deljenje je namreč kar množenje z recipročnim elementom. Če le-tega označimo z \(x\), potem velja \(a\cdot x \mod p =1\), zato ga lahko poiščemo kot rešitev diofantske enačbe \(ax+py=1\) z razširjenim Evklidovim algoritmom (glej članek M. Juvana, O Evklidovem algoritmu, Presek 21 (1993-94), str. 116-121). Ta enačba je vedno rešljiva, saj sta si \(a\) in \(p\) tuja.
Izrek 1. Od nič različen polinom stopnje \(n\) ima v obsegu največ \(n\) ničel.
Zgornji izrek ne velja vedno, če koeficienti polinoma niso iz obsega. Na primer v kolobarju \(\mathbb{Z}_6\) zgornja trditev ne drži, saj ima kvadratni polinom \(f(x)=(x-1)x\) kar štiri ničle: \(0,1,3,4\). Za prvi dve ničli potrebujemo prisotnost le po enega faktorja, za zadnji dve pa potrebujemo hkrati oba faktorja. V obsegih pa je produkt lahko nič le tedaj, ko je vsaj en izmed faktorjev enak nič. Če je \(a\) ničla polinoma \(f(x)\), potem nam razcep \[ x^i-a^i=(x-a)(x^{i-1}+ \cdots +a^{i-1}) \] zagotavlja, da lahko zapišemo \(f(x)=f(x)-f(a)=(x-a)q(x)\), kjer je \(q(x)\) polinom stopnje \(n-1\). Torej se nam za vsako ničlo, ki jo izpostavimo, zmanjša stopnja preostanka za 1 in zato število ničel res ne more preseči stopnje polinoma.
Naj bo \(p\) neko dovolj veliko praštevilo (\(p \ge n+1\)), \(K\in \mathbb{Z}_p\) (skrivnost) in \({\cal P}=\{P_1,\dots,P_n\}\) množica oseb, ki jim želimo razdeliti skrivnost.
Delivec \(D \notin {\cal P}\) izbere \(n\) različnih elementov \(x_1,x_2,\dots,x_n\in \mathbb{Z}_p\backslash \{0\}\) in dodeli del \(x_i\) osebi \(P_i\in {\cal P}\) (vrednosti \(x_i\) so lahko javne).
Za delitev ključa \(K\) delivec \(D\) naključno in neodvisno izbere \(t\!-\!1\) elementov \(a_1,\dots,a_{t-1}\!\in\!\mathbb{Z}_p\) ter izračuna \(y_i=a(x_i)\) \((1\le i\le n)\), kjer je \[ a(x) = K + a_1x +\cdots +a_{t-1}x^{t-1} \ \mod p, \] in da del \(y_i\) osebi \(P_i\).
Primer: Naj bo \(p=17\), \(t=3\) in \(n=5\). Za javne koordinate \(x\) izberimo \(x_i=i\), \(1\le i \le 5\). Predpostavimo, da osebe \(P_1\), \(P_3\) in \(P_5\) združijo svoje dele, ki so zaporedoma enaki \(8\), \(10\) in \(11\). Če vzamemo \(a(x)=a_0+a_1x+a_2x^2\) in izračunamo \(a(1)\), \(a(3)\) ter \(a(5)\), dobimo sistem treh linearnih enačb v \(\mathbb{Z}_{17}\):
\[ \begin{array}{ccc} a_0 +\ \ \! a_1 + \ \ \! a_2 &=& \ \ \! 8, \\[-2mm] a_0 + 3a_1 + 9a_2 &=& 10, \\[-2mm] a_0 + 5a_1 + 8a_2 &=& 11, \end{array} \]
ki ima v \(\mathbb{Z}_{17}\) enolično rešitev \(a_0=13\), \(a_1=10\) in \(a_2=2\). Ključ je torej enak \(K=a_0=13\).
V primeru splošne Shamirjeve sheme osebe \(P_1,P_2,\dots,P_t\) določijo ključ \(K\) iz enačb: \[ y_i=a(x_i)=a_0+a_1x_i+\dots +a_{t-1}x_i^{t-1}\ \ \ \ (1\le i\le t). \] Koeficienti tega sistema tvorijo Vandermondovo matriko z determinanto \[ \bigl( (x_t -x_1) \cdots (x_t -x_{t-1}) \bigr) \bigl( (x_{t-1}-x_1) \cdots (x_{t-1}-x_{t-2}) \bigr) \cdots \bigl( (x_3-x_1) (x_3-x_2)\bigr) (x_2-x_1), \] ki je po modulu \(p\) različna od 0, zato ima sistem enolično rešitev v \(\mathbb{Z}_p\). Ker pa tak pristop močno presega okvire osnovnošolske in tudi srednješolske matematike, zaslužil pa bi tudi vsaj poseben članek o determinantah in sistemih linearnih enačb, si raje oglejmo drugi način.
Pomagamo si s polinomom \(p(x)\) stopnje največ \(t\!-\!1\), ki ga zna izračunati vsaka skupina \(t\) oseb iz svojih delov. Poznamo ga pod imenom interpolacijski polinom (glej sliko 2) in ga vpeljemo prek polinomov
\(p_i(x)= (x-x_1)(x-x_2)\cdots (x-x_{i-1})(x-x_{i+1})\cdots (x-x_t)\), tj. produktov faktorjev \((x-x_j)\) za \(j\ne i\): \[
p(x)= y_1 {p_1(x) \over p_1(x_1)} +\cdots + y_t {p_t(x) \over p_t(x_t)}.
\]
Slika 2
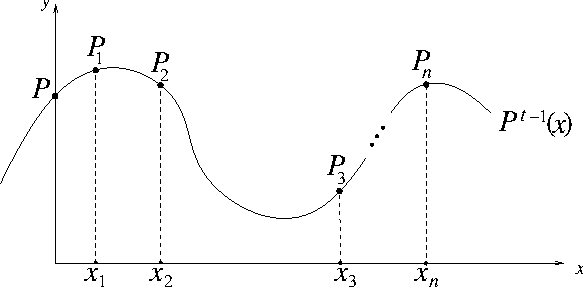
- Interpolacijski polinom.
Faktor v \(i\)-tem sumandu ob \(y_i\) zavzame vrednost \(1\) za \(x=x_i\) in \(0\) za vsak drug \(x_j\). Z neposrednim računom ugotovimo, da velja \(p(x_i)=a(x_i)\), \(i=1,\dots,t\). Od tod sledi, da ima polinom \(p(x)-a(x)\), ki je stopnje kvečjemu \(t\!-\!1\), vsaj \(t\) ničel. Izrek 1 nam potem zagotovi, da je to možno le, kadar sta polinoma \(a(x)\) in \(p(x)\) enaka. Zato je \(K=p(0)\).
Da se prepričamo, da je to res \((t,n)\)-stopenjska shema za deljenje skrivnosti, moramo utemeljiti še, da \(t-1\) oseb ne more izključiti nobenega ključa. Če k \(t\!-\!1\) osebam (te poznajo \(t\!-\!1\) delov skrivnosti) dodamo za poljuben \(a_0\in \mathbb{Z}_p\) še del \(y_0=a_0\), ki predstavlja vrednost polinoma \(a(x)\) v točki \(x_0=0\), potem z zgornjo formulo zopet dobimo polinom \(a(x)\), ki ustreza vsem podatkom, ki so trenutno na voljo.
Ko želi skupina \(t\) oseb izračunati ključ \(K\) iz svojih delov, pravzaprav ne potrebuje celotnega polinoma \(p(x)\), pač pa samo vrednost: \[ K= y_1 {p_1(0) \over p_1(x_1)} +\cdots + y_t {p_t(0) \over p_t(x_t)}. \] Od tod se lepo vidi, da je iskani ključ linearna kombinacija delov \(y_i\): \(K=b_1 y_1 +b_2 y_2+\cdots +b_t y_t\), kjer je \[ b_i= {p_i(0) \over p_i(x_i)} = {x_1 x_2 \cdots x_{i-1} x_{i+1} \cdots x_t \over (x_1-x_i)(x_2-x_i)\cdots (x_{i-1}-x_i)(x_{i+1}-x_i)\cdots (x_t-x_i)}, \] torej je bila \((t,t)\)-stopenjska shema za deljenje skrivnosti le poseben primer splošne sheme. Še več, za samo uporabo splošne sheme za deljenje skrivnosti v resnici ne potrebujemo ne računanja interpolacijskih polinomov ne reševanja sistemov enačb, temveč le seštevanje, množenje in deljenje v končnem obsegu.
Nadaljevanje primera: Osebe \(P_1\), \(P_3\) in \(P_5\) lahko izračunajo \(b_1\), \(b_3\), \(b_5\) po zgornji formuli. Če izračunamo recipročne elemente z razširjenim Evklidovim algoritmom, dobimo: \[ b_1 = { x_3 x_5 \over (x_3-x_1)(x_5-x_1)} \ \mod 17 = 3 \cdot 5 \cdot 2^{-1} \cdot 4^{-1} \ \mod 17 = 4. \] Podobno izračunamo tudi \(b_3=3\) in \(b_5=11\) ter za dele \(8\), \(10\) in \(11\) dobimo \[ K = 4 \cdot 8 + 3 \cdot 10 + 11 \cdot 11 \ \mod 17 = 13. \]
Za konec poudarimo, da je varnost Shamirjeve sheme za deljenje skrivnosti brezpogojna, tj. noben ključ ni na podlagi informacij, ki jih imajo nepooblaščene množice, bolj verjeten od drugega. Možne so seveda še razne posplošitve, kot je dodelitev različnih prioritet različnim osebam (npr. za dostop do vojaške skrivnosti sta potrebna dva generala ali pet majorjev) ipd., a to je že druga zgodba. Več o deljenju skrivnosti si radovedni bralec lahko poišče v učbeniku D.R. Stinsona, Cryptography – Theory and Practice, CRC Press, 1995 ali pa dipomskem delu (FMF) Vanje Seničar.
8.5 Par izbira film po medmrežju
Ana in Bob gresta na zmenek. Ana si želi ogledati en film, Bob pa si želi ogledati drugega. Odločita se, da z metanjem kovanca izbereta film. Če pade »cifra«, bosta šla gledat film po Anini izbiri; v nasprotnem primeru bosta šla gledat film po Bobovi izbiri. Ko sta Ana in Bob v neposredni bližini, je to enostavno: eden izmed njiju, recimo Bob, vrže kovanec in oba preverita rezultat. Ko pa sta daleč narazen in govorita po telefonu, je to težje. Bob lahko po menu obrne kovanec na svojo stran in pove Ani rezultat, vendar Ana nima razloga, da bi verjela izidu. Bob bi lahko preprosto trdil, da je kovanec padel na stran cifra in Ana tega ne bi mogla preveriti. To zagotovo ni najboljši način za začetek zmenkovanja. Preprosta rešitev njunega problema uporablja kriptografski primitiv, ki mu bomo rekli zavezujoč bit. Omogoča, da se Bob zaveže, da bo \(b_0 \in \{0, 1\}\) po svoji lastni izbiri. Kasneje lahko Bob odpre zavezo in prepriča Ano, da je \(b\) vrednost, za katero se je zavezal. Zavezanost za bit \(b\) povzroči niz zaveze \(c\), ki ga Bob pošlje Ani, in odpiralni niz, ki ga Bob uporabi za poznejše odpiranje obveznosti. Shema zavezanosti je varna, če izpolnjuje naslednji dve lastnosti: Skrivanje: Zavezujoči niz \(c\) ne razkrije informacij o vnesenem bitu \(b\). Natančneje, porazdelitev na \(c\) pri prevzemu na bit \(0\) se ne razlikuje od porazdelitve na \(c\) pri prevzemu na bit \(1\). V shemi zavezanosti bit predstavljamo vezalno lastnost, ki temelji na varnosti določenega PRG \(G\).
Vezanje: Naj bo \(c\) niz vrstic, ki jih je Bob ustvaril. Če Bob lahko zavezo odpre kot nekaj \(b_0 \in \{0, 1\}\), potem je ne more odpreti kot \(\overline{b}\).
To zagotavlja, da ko se Bob nekaj zaveže, ga lahko odpre kot \(b\) in nič drugega. V shemi zavezanosti predstavljamo zavezujočo lastnost brezpogojno. Naj bo to Bobov izhodiščni niz. Če Bob lahko zavezo odpre kot nekaj \(b_0 \in \{0, 1\}\), potem je ne more odpreti kot \(\overline{b}\). To zagotavlja, da ko se Bob nekaj zaveže, ga lahko odpre kot \(b\) in nič drugega. V shemi obveznosti predstavljamo zavezujoče premoženje brezpogojno.
Metanje kovanca. S shemo zavezanosti lahko Ana in Bob ustvarita naključni bit \(b_0 \in \{0, 1\}\), tako da nobena stran ne more spremeniti rezultata v svoj želeni rezultat, ob predpostavki, da se protokol uspešno konča. Takšne protokole imenujemo protokoli za metanje kovancev. Nastali bit \(b\) določa kakšen film si gresta ogledat. Ana in Bob uporabljata naslednji preprost protokol za metanje kovanca:
- Korak 1: Bob izbere naključni bit bit \(`b_0 \in_R \{0, 1\}`\), Ana in Bob izvršita protokol zaveze, s katerim Ana pridobi zavezo \(c\) do \(b_0\) in Bob pridobi uvodni niz \(s\).
- Korak 2: Ana izbere naključni bit \(`b_1 \in_R \{0, 1\}`\) in \(`b_1`\) pošlje Bobu na prosto.
- Korak 3: Bob odpre zavezo, tako da Ana razkrije b0 in s. Ana preveri, ali je \(c\) res zaveza \(b_0\) in prekine, če preverjanje ne uspe.
- Izhod: dobljeni bit je \(`b := b_0 \mathbin{\oplus} b_1`\).
Če se protokol uspešno konča in ena stran pošteno sledi protokolu, potem druga stran ne more prilagoditi rezultata k svojemu želenemu izidu.
Oseba 1: Oseba 2:
8.6 Problem bizantinskih generalov
Literatura
“Protocol.” 2018. Cambridge Dictionary. Cambridge University Press 2019. https://dictionary.cambridge.org/dictionary/english/protocol.