Poglavje 7 Podpisi

Uvod: TO-DO

7.1 Diffie-Hellmanov dogovor o ključu

Ali je možno, da se dve osebi, ki se želita pogovarjati po javnem kanalu (npr. telefonu ali Internetu), preko njega dogovorita o skrivnem ključu?

Le-tega naj bi poznali samo oni dve in ga potem uporabili za šifriranje njunega pogovora. Če sta se že prej srečali na štiri oči, potem bi se gotovo lahko spomnili nečesa, kar je skupno le njima in na osnovi tega sestavili skrivni ključ. Dovolj je na primer že, da se spomnita neke knjige, ki sta jo takrat skupaj občudovali, in že si lahko izbereta za relativno varno geslo npr. deveti odstavek v tretjem poglavju. Četudi bi prisluškovalec vedel, da gre za deveti odstavek v tretjem poglavju, nikakor ne bi mogel ugotoviti, za katero knjigo gre in mu tako pridobljena informacija brez knjige ne bi bila v kdo ve kakšno pomoč. Naj zveni še tako čudno, a ljudje so dolga leta uporabljali prav takšne kodne knjige za zaščito svojih zaupnih pogovorov. Danes, v času, ko so pri Googlu začeli skenirati skoraj vse knjige po vrsti in ko se da prav hitro preveriti več milijonov gesel, pa tak pristop ni nujno dovolj varen.

Kaj pa če se naši osebi nista še nikoli srečali na štiri oči ali pa če je bil poleg njiju (oziroma na javnem kanalu) vedno še nekdo, ki jima utegne kaliti srečo (glej sliko 1)? Ali se lahko potem preko javnega kanala dogovorita o skupnem ključu, ki je znan le njima?

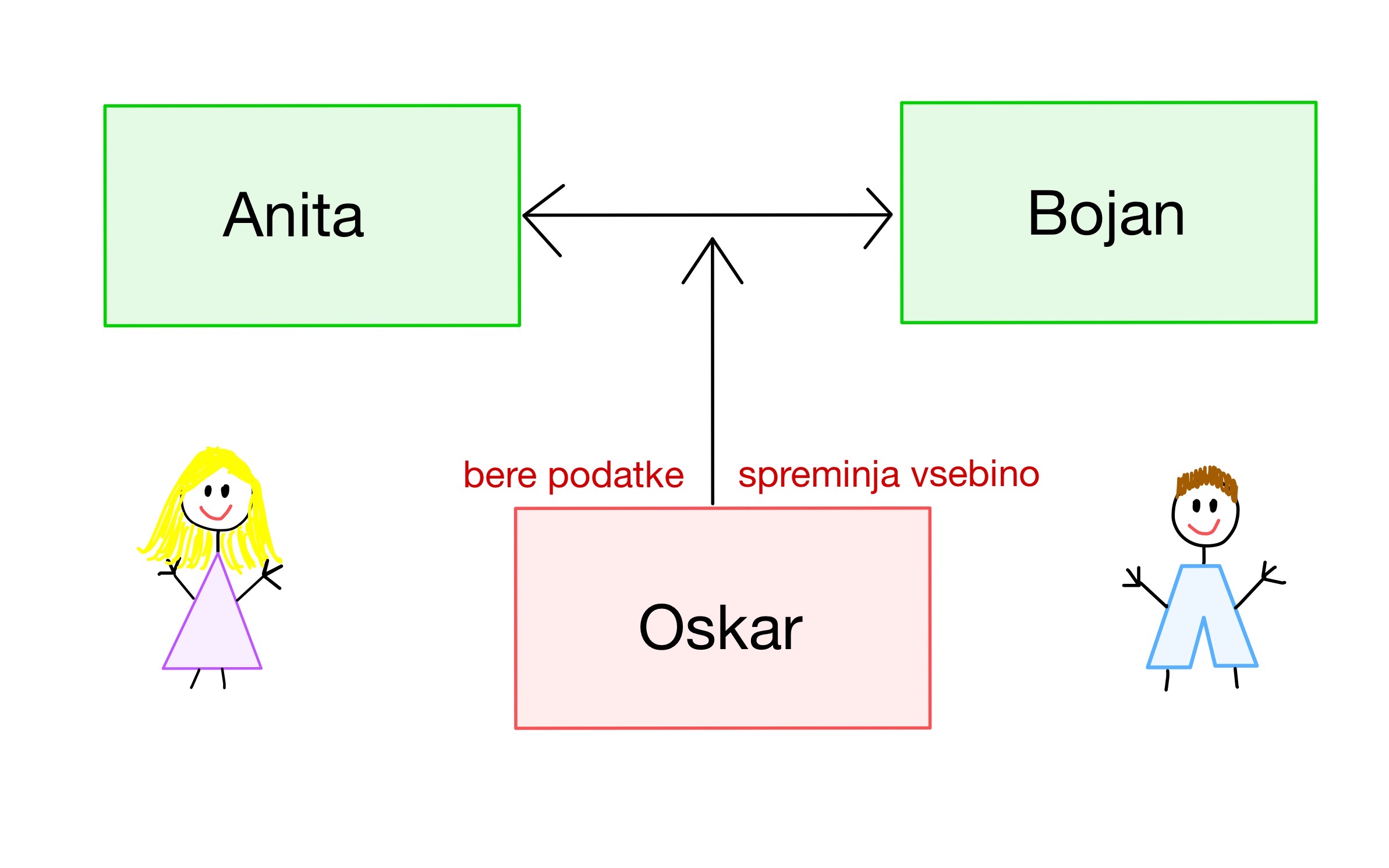
Slika 1. Anita, Bojan ter napadalec Oskar.

Rekli boste, da je to vendar nemogoče, saj s strani enega sogovornika ni mogoče ločiti drugega sogovornika od prisluškovalca, ki je slišal prav vse, kar je drugi sogovornik povedal oziroma slišal. Na našo srečo je tak dogovor o ključu iskal tudi Whitield Diffie. Verjel je, da so ga v črnih kabinetih (ki so jih za potrebe lastne varnosti in vohunjenja ustanovile različne države) že našli in da si ne želijo, da bi o njem vedeli običajni ljudje. Ena izmed največjih takih organizacij je ameriški NSA (No Such Agency – morda že veste, kaj ta kratica pomeni v resnici). Tam dela največ matematikov na svetu, vendar pa so rezultati njihovega dela strogo zaupne narave in jih uporabljajo v vojaške oziroma vohunske namene. Diffija je bilo kar groza, da bi na ta način zadrževali razvoj vsega človeštva. Zato si je zadal za osrednjo nalogo, da se bo priboril do teh skrivnosti in jih dal na voljo vsem ljudem. Temu cilju je podredil svoje življenje. Kriptologi so ga imeli večinoma že za malce trčenega, saj niso verjeli, da je kaj takega sploh možno. Ko je Diffie nekega dne izvedel, da se z istim problemom ukvarja tudi Martin Hellman, ki je živel na čisto drugem koncu ZDA, se je nemudoma usedel v avto in se z vzhodne obale odpravil živet v njegovo bližino (San Francisco). Sledilo je obdobje skupnega iskanja rešitve in čez nekaj let se jima je zares posrečilo.

Slika 2. Whitfield Diffie.

Najprej sta rešila Diffijev problem, ki je osrednja tema tega sestavka, kmalu zatem pa so skupaj z Ralphom Merklom prišli do revolucionarnega koncepta kriptosistemov z javnimi ključi, ki ga bomo spoznali v tretjem delu. Čeprav so rešitev iskali tako dolgo, pa se je Diffie-Hellmanov dogovor o ključu (na kratko DH-protokol) izkazal za zelo enostavnega in elegantnega. Predstavimo ga!

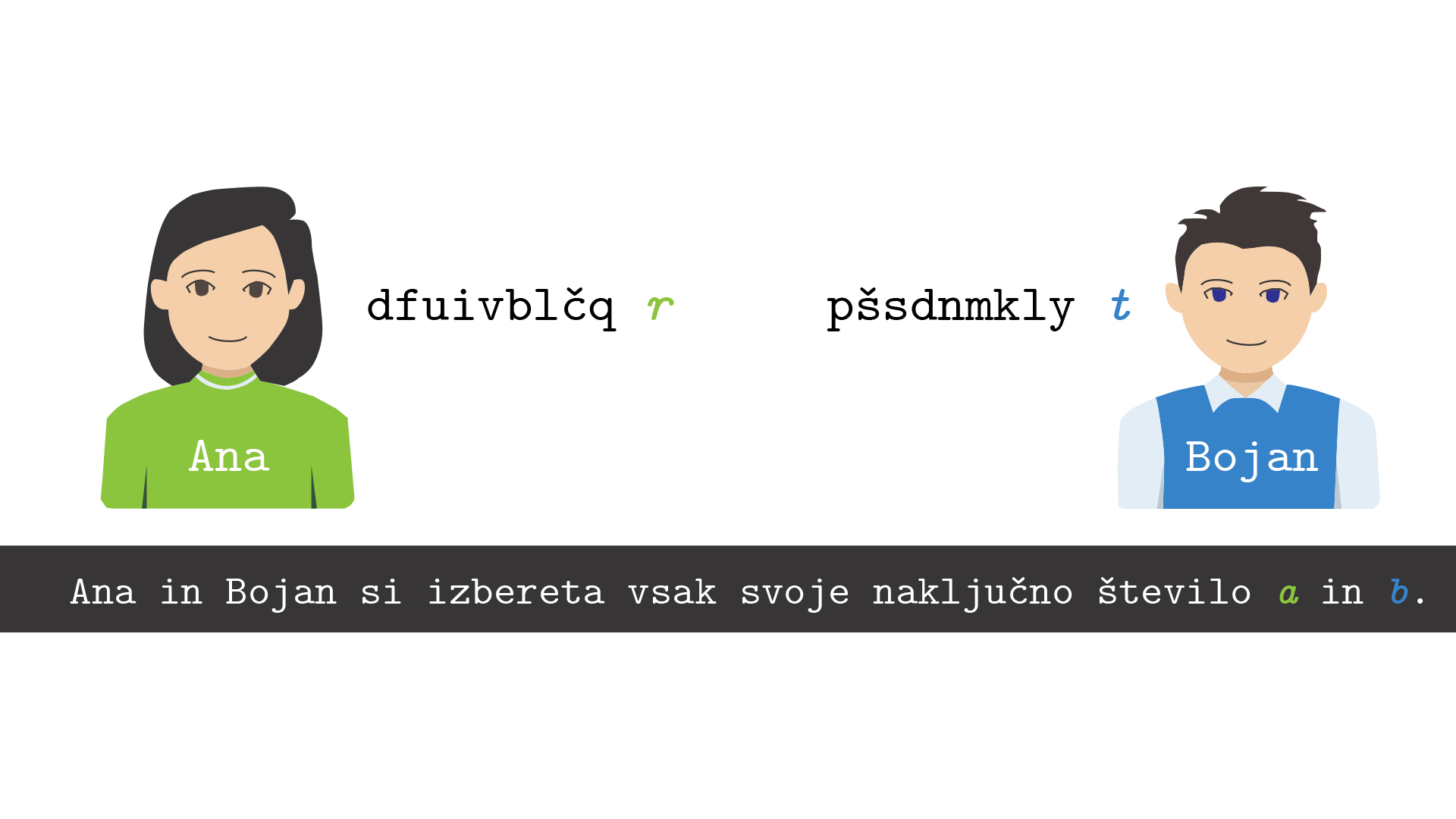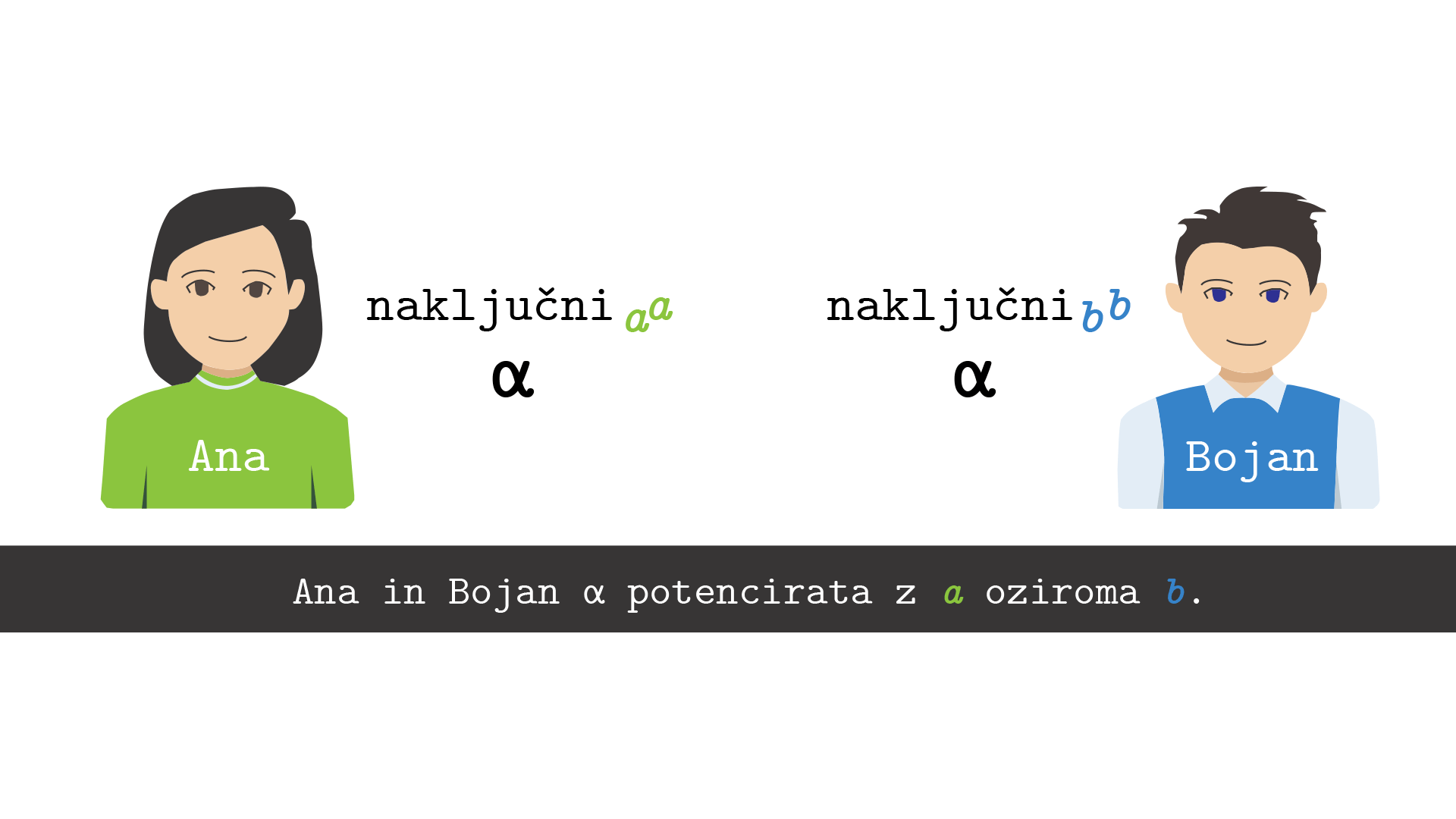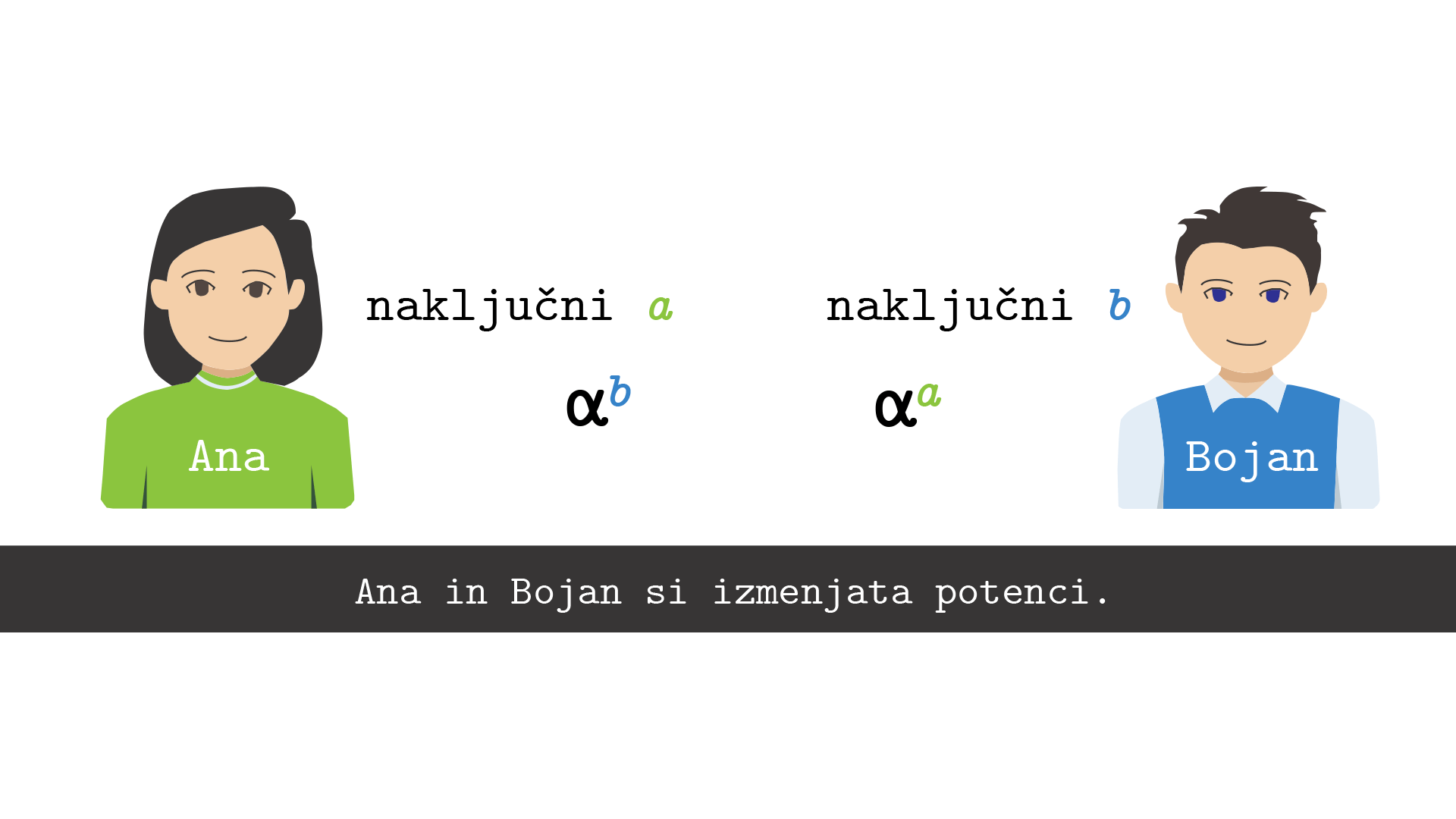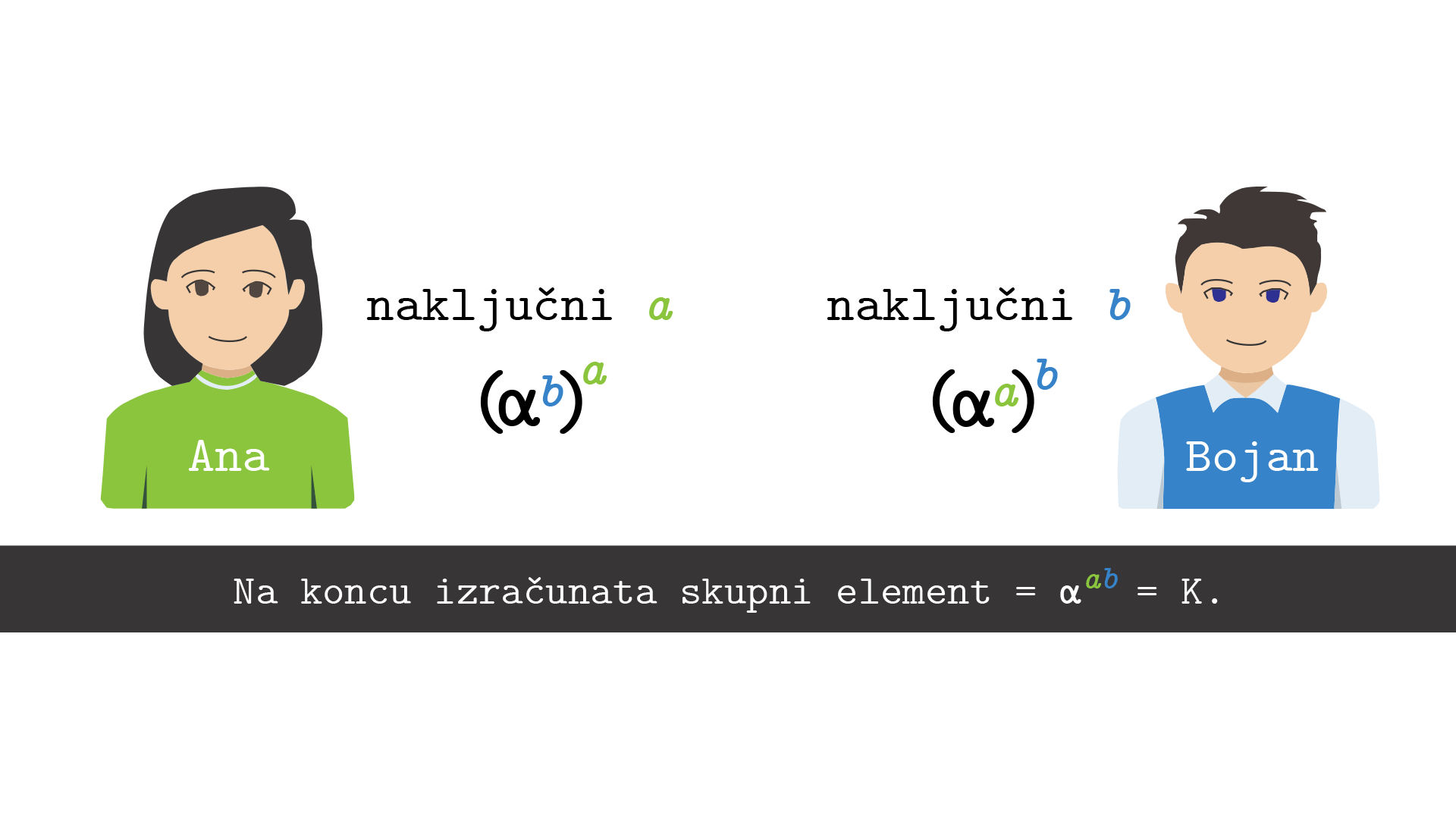
Najprej se Anita in Bojan dogovorita, kako bosta računala, na primer katero število $\alpha$ bosta uporabljala. Takemu številu

bomo rekli generator in kmalu bo postalo jasno, zakaj je tako. Anita si naključno izbere svoje zasebno število $a$, Bojan pa svoje naključno zasebno število $b$. Nato izračunata vsak svojo potenco $A:=\alpha^a$ ter $B:=\alpha^b$ ter si ju izmenjata preko javnega kanala. Končno izračunata skupni tajni ključ $\alpha^{ab}=K=\alpha^{ba}$, Anita z $B^a=(\alpha^b)^a$, Bojan pa z $A^b=(\alpha^a)^b$. Glej sliko 4.

Slika 3. Martin Hellman.

Diffie-Hellmanov dogovor o ključu - Anita in Bojan si izbereta vsak svoje naključno število $a$ in $b$ ter si na koncu delita skupni ključ, ki ga izračunata iz izmenjanih potenc: $(\alpha^a)^b = (\alpha^b)^a = \alpha^{ab}=K$.

Če je bil namen dogovora o ključu med Anito in Bojanom pošiljanje zaupnega sporočila, potem po zgoraj opisanih dveh izmenjavah sledi še tretja, v kateri Anita s skupnim tajnim ključem zašifrira in pošlje zaupno sporočilo, ki ga na drugi strani Bojan brez težav odšifrira. Popolnoma brez matematike lahko opišemo podoben protokol, ki sta ga predlagala Massey in Omura. Tudi zanj potrebujemo tri izmenjave sporočil. Glej škatlo Protokol Massey-Omura. V digitalnem svetu, kjer si seveda ne želimo fizičnih ključavnic, % Če pa želimo tak protokol izvesti brez fizičnih ključavnic, si namesto njih lahko omislimo dve obrnljivi funkciji, ki med seboj komutirata, tj. velja pravilo o zamenjavi.

Protokol Massey-Omura

korak: Anita zaklene sporočilo v škatlo s svojo ključavnico ter vse skupaj pošlje Bojanu.
korak: Bojan prejme pošiljko, prepozna Anitino ključavnico, doda še svojo ključavnico in vrne pošiljko Aniti.
korak: Anita prejme pošiljko, prepozna svojo in Bojanovo ključavnico ter odklene in odstrani svojo ključavnico. Nato še drugič pošlje pošiljko Bojanu.
korak: Bojan prejme pošiljko, odklene in odstrani svojo ključavnico ter pride do sporočila.

Učinkovitost

Zakaj je DH-protokol dobra rešitev Diffievega problema? Za začetek preverimo ali znamo učinkovito izvesti vse potrebne računske operacije. V našem primeru je to potenciranje elementa $\alpha$.

Če želimo izračunati $\alpha^n$, kjer je $n\in \mathbb{N}$, potem lahko to storimo z $n-1$ množenji: \[ ((\cdots((\alpha*\alpha)*\alpha)*\cdots)*\alpha)*\alpha. \] Žal s tem ne moremo biti zadovoljni, saj čas računanja merimo v odvisnosti od dolžine zapisa števil, s katerimi imamo opravka. Naj bo dolžina največjega zapisa enaka $k$. Produkt dveh števil v dvojiškem zapisu lahko izračunamo v grobem s $k^2$ operacijami (premisli zakaj!). Problem pa je v tem, da iz \[ 2^k\approx n % \mbox{ (oziroma $\log_2 n \approx k$)} \] sledi, da moramo opraviti eksponentno mnogo množenj. Eksponentni algoritmi so izredno počasni (glej škatlo Zgodba iz antične Indije), v praksi pa je pogosto $k>100$, tako da takšno računanje potence v nobenem primeru ne pride v poštev.

Zgodba iz antične Indije

O njej smo v Preseku že pisali (A. Lipovec, Kaj imajo skupnega Gari Kasparov, Jamie Oliver in ozonske luknje? Presek 33 (2005), str. 4-6), zato le na kratko omenimo, da naj bi na prvo polje šahovnice položili eno zrno riža, na drugo polje dve, na tretje štiri … (za vsako naslednje polje podvojimo število zrn). Šahovnica ima 64 polj, kar pomeni, da bi morali nanjo postaviti \[ 1+2+2^2+\cdots+2^{63}=2^{64}-1\ \ \mbox{zrn riža}. \] Za kriptografijo je zelo pomembno, da razumemo velike številke. Ali si lahko predstavljamo vsaj v grobem koliko riža bi to bilo? Recimo, da lahko poje povprečen človek pol kg riža na dan. To je kar precej, ko je riž enkrat kuhan. Koliko zrn napolni čajno žličko? Približno 330, za pol kg riža pa jih potrebujemo nekaj čez 80 oziroma $27.500=2,75*10^4$ zrn riža. Na svetu je danes 6,6 milijarde $=6,6 * 10^9$ ljudi. Če bi vsi ljudje jedli samo riž, bi torej lahko pojedli $2,75*10^4 * 6,6* 10^9\approx 1,8* 10^{14}$ zrn riža na dan.
Sedaj pa se vrnimo k številu $2^{64}-1\approx 1,8*10^{19}$ zrn in ga delimo s številom $1,8\times 10^{14}$ zrn, ki jih poje človeštvo na dan. Dobimo $100.000$ dni, kar pomeni, da bi lahko svet jedel riž s šahovnice toliko časa, dan za dnem, oziroma $100.000/365\approx 274$ let!

Pa si poglejmo zapis števila $n$ v dvojiškem sistemu: \[ n = n_k\, 2^k +\cdots+ n_1\, 2^1 + n_0\,2^0, \ \ \ \ \ \ \mbox{kjer je $n_i\in \{0,1\}$}. \] Potem je \[ \alpha^n=\alpha^{n_k\,2^k}*\cdots * \alpha^{n_1\,2^1}*\alpha^{n_0\,2^0}. \] Potence $\alpha^2,\alpha^{2^2},\dots,\alpha^{2^k}$ izračunamo s $k$ kvadriranji (v ta namen kvadriramo $\alpha^{2^{i-1}}$, da dobimo $\alpha^{2^i}$). S tem smo dobili vse faktorje v zgornji identiteti. Potem pa za izračun produkta iz () potrebujemo še največ $k$ množenj. Skupaj nanese $2k$ množenj oziroma v grobem $k^3$ procesorskih operacij, kar pomeni, da je naše računanje učinkovito in s tem tudi DH-protokol.

Varnost

Kako pa je z možnimi napadi na DH-protokol?

(Mlajši bralci, ki se še niste srečali s funkcijami, lahko mirno preskočite ta razdelek.)

Na prvi pogled se zdi, da je dovolj, da znamo učinkovito izračunati bodisi $\log_{\alpha} A=a$ bodisi $\log_{\alpha} B=b$. Če bi bila $\alpha$, $a$ in $b$ realna števila, potem to ne bi smel biti problem – vsaj od takrat naprej, ko so ljudje sestavili dobre logaritemske tablice, da o današnjih računalnikih niti ne govorimo. Vendar pa si kriptografi namesto obsega realnih števil v praksi raje izberemo diskretno grupo, v kateri ne znamo učinkovito izračunati logaritma poljubnega njenega elementa. Glej škatlo Problem diskretnega logaritma (DLP). Spomnimo se, da smo pred leti v Preseku pisali o računalih nove dobe (1 del, Presek 30/1 (2002-03), 226-231 in 2. del, Presek 30/5 (2002-03), 291–296), kjer smo vpeljali nekaj zanimivih grup. Pa DLP ni edini razlog za uporabo diskretnih grup. Če računamo z običajnimi tipi števil, celimi, racionalnimi ali realnimi števili, se zna zgoditi, da bodo rezultati izračunov hitro zrastli preko vseh meja (glej škatlo Zgodba iz antične Indije) ali pa bomo zaradi omejene velikosti prisiljeni nenehno zaokrožati. V kriptografiji je učinkovitost osrednjega pomena, približki pa ne zadoščajo (predstavljajte si, da vam bankomat ali pa žepni telefon odgovorita, da danes nista povsem zadovoljna z vašim geslom, pa naj si bo to zato, ker še vedno računata ali pa se jima zdi geslo samo približno prav).

Tako si za računanje raje omislimo končne množice kot pri številčnici na uri. Tak zgled so kolobarji $\mathbb{Z}_n$, $n\in \mathbb{N}$, v katerih računamo po modulu števila $n$. Za elemente vzamemo $\{0,1,\dots,n-1\}$, računamo pa tako, da seštejemo ali zmnožimo dve števili tako, da pravi rezultat nadomestimo z njegovim ostankom pri deljenju z modulom $n$. Na primer za $n=7$ velja $4+_7 5 = 4+5 \ \mod 7 =2$ in $5*_7 4= 5\cdot 4 \ \mod 7 =6$, saj ima vsota 9 ostanek 2 pri deljenju s 7, produkt 20 pa ostanek 6, glej sliko 3.

Slika 5

Računanje po modulu 7.

Če želimo še deliti z vsakim neničelnim številom, potem si moramo za modul $n$ izbrati neko praštevilo $p$, tako da v resnici delamo v praštevilskem obsegu $\mathbb{Z}_p$ oziroma za potrebe DH-protokola kar v njegovi podgrupi $(\mathbb{Z}_p\backslash \{0\},*)$, ki ji pravimo multiplikativna podgrupa, oznaka $\mathbb{Z}_p^*$. Potem vsak element $\alpha\in \mathbb{Z}_p^*$, za katerega velja $D(\alpha,p-1)=1$, potence $\alpha,\alpha^2,\dots,\alpha^{p-1}$ pretečejo vse elemente grupe $\mathbb{Z}_p^*$ (zadnji element je seveda enota, saj Fermatov izrek za izbrana $\alpha$ in $p$ pravi $\alpha^{p-1}\equiv 1 \pmod p$, glej članek D. Pagona, Kongruence in Eulerjev izrek, Presek 15 (1987-88), str. 194–196), tj. $\alpha$ generira grupo $\mathbb{Z}_p^*$. Multiplikativna grupa poljubnega končnega obsega je torej ciklična, tj. v grupi obstaja tak element, da so vsi elementi njegove potence, zato lahko njene elemente predstavimo na krogu, tako kot smo to storili na sliki 5.

Problem diskretnega logaritma (DLP)

Za dano grupo $G$ in elementa $\alpha, \beta \in G$, kjer je red elementa $\alpha$ enak $n$, poišči učinkovito metodo, ki določi celo število $x$, $0 \leq x \leq n-1$ (če obstaja), tako da je $\alpha^x = \beta$. Število $x$ imenujemo diskretni logaritem števila $\beta$ pri osnovi $\alpha$.

Požrešna metoda za reševanje DLP, ki računa zaporedne potence elementa $\alpha$, tj. $\alpha,\alpha^2,\alpha^3,\dots$ in jih primerja z $\beta$, je včasih znala odpovedati tam nekje za $n$ nad $2^{40}$, danes pa verjetno tam nekje pri $2^{80}$ (odvisno koliko opreme in časa imamo na voljo).

Metoda mali-veliki korak je v nekaterih grupah še vedno najboljša metoda (izboljšati se da le njeno prostorsko zahtevnost) in odpove pri dvakrat večjih eksponentih, ki smo jih omenili pri požrešni metodi. Pri tej metodi si najprej naredimo tabelo na enak način, kot smo začeli pri požrešni metodi, le da se ustavimo pri $k$-ti potenci, kjer je $k$ celi del kvadratnega korena iz $n$ (lahko si predstavljamo, da smo z malimi koraki prehodili in s tem pokrili lok dolžine $k$ na zgoraj omenjenem krogu, ki ga sestavljajo potence elementa $\alpha$). Nato pa zaporedoma pregledujemo katerega izmed elementov $\beta, \beta\alpha^k,\beta\alpha^{2k}\dots,\beta\alpha^{k*k}$ najdemo v tej tabeli (enega bomo zagotovo, saj pravkar omenjenega loka ne moremo preskočiti s korakom dolžine $k$). Ko se to zgodi, velja \[ \beta (\alpha^k)^j=\alpha^i, \] od koder dobimo $\log_{\alpha} \beta =i-k*j \ \mod n$.

Morda izgleda na prvi pogled, da bi lahko namesto $\mathbb{Z}_p^*$ uporabljali kar grupo $(\mathbb{Z}_n,+_n)$, $n\in \mathbb{N}$. Potem bi namesto potence $\alpha^a$ v DH-protokolu zapisali večkratnik $V=a\alpha$, kjer je $\alpha\in \mathbb{Z}_n$, $D(\alpha,n)=1$ in $a\in \mathbb{N}$. Vendar pa v tem primeru poznamo algoritem, ki nam iz večkratnika $V$ izračuna $a$. V ta namen je namreč potrebno rešiti naslednjo diofantsko enačbo: \[ a\alpha + k n =1, \] za $a$ (in $k$). To pa znamo učinkovito rešiti z razširjenim Evklidovim algoritmom, saj je $D(\alpha,n)=1$ (glej članek M. Juvana, O Evklidovem algoritmu, Presek 21 (1993-94), str. 116-121). Izbira najboljše grupe $G$ za DH-dogovor o ključu, v kateri bo računanje potenc učinkovito, reševanje DLP pa nedosegljivo, je izredno občutljiva naloga, ki jo morajo opraviti izkušeni kriptologi.

Aktivni srednji napadalec

Zgoraj predstavljen Diffie-Hellmanov protokol imenujemo tudi neoverjen Diffie-Hellmanov protokol. Pri njem udeleženci namreč ne morejo z gotovostjo ugotoviti izvora javnih vrednosti ostalih udeležencev (tj. potenc, ki si jih morajo izmenjati). To pa naredi neoverjen Diffie-Hellmanov protokol ranljiv na napad, ki ga imenujemo napad srednjega napadalca (angl. middle man attack), glej sliko 6.

Slika 6

Napad srednjega napadalca na DH-protokol.

Pri tem napadu nasprotnik Oskar prestreže Anitino javno vrednost $\alpha^a$ in pošlje svojo javno vrednost $\alpha^{a'}$ Bojanu. Ko Bojan pošlje svojo javno vrednost $\alpha^{b}$, jo Oskar prestreže in zamenja s svojo javno vrednostjo $\alpha^{b'}$ in jo pošlje naprej Aniti. Tako delita Anita in Oskar skupen skrivni sejni ključ $K_{ab'}=\alpha^{ab'}$ ter Bojan in Oskar drug skrivni sejni ključ $K_{a'b} =\alpha^{a'b}$. Po tej izmenjavi Oskar preprosto odšifrira sporočila poslana s strani Anite ali Bojana, jih prebere in po potrebi spremeni, preden jih zopet zašifrira in pošlje naprej.

Besedna zveza napad srednjega napadalca se uporablja za opis napada, kadar Oskar sedi nekje na sredini komunikacijskega kanala/poti med Anito in Bojanom ter oba prelisiči. Je pomemben napad, zaradi katerega je potrebno dopolniti in spremeniti številne komunikacijske protokole. Vendar pa je, kot pravi B. Schneier, to tudi napad, ki ga lahko uporabimo v vsakdanjem življenju:

Kaj se je zgodilo v zgornjem primeru?

Navidezna gospa-pomočnica se je postavila na sredino komunikacije med pravo pomočnico ter pravo gospo in se predstavila vsaki kot tista druga. Pomočnica pošlje priporočila nekomu, ki ni prava gospa. Prava gospa preveri priporočila, ne da bi preverila, da v resnici ne pripadajo lažni pomočnici.

Napad srednjega napadalca je uspešen zato, ker Diffie-Hellmanov protokol ne preveri identitete udeležencev v protokolu oziroma njihovih javnih vrednosti. Rešitev tega problema lahko dosežemo tako, da se udeleženci in javne vrednosti, ki nastopajo v protokolu, ustrezno overijo z digitalnimi certifikati. To pa je že nova zgodba, ki si jo lahko ogledate v tretjem delu hkrati z zgodbo o volku in sedmih kozličkih.

Naloge

Funkcija $f(x)=\log_{\alpha}x$ nam pove, kateri eksponent moramo uporabiti na $\alpha$, da dobimo $x$. Določi definicijsko območje realnih funkcij $f(x)$ in $g(y)=\alpha^y$. Prepričaj se, da je $\alpha^{\log_{\alpha}x}=x$ in $\log_{\alpha}(\alpha^x)=x$, kar pomeni, da sta funkciji $f(x)$ in $g(x)$ inverzni.

ODGOVOR
Preveri enakost \[ 1+2+2^2+\cdots+2^{63}=2^{64}-1, \] tako da levo stran pomnožiš z $(2-1)$ in odpraviš oklepaje. Bi znal to enakost posplošiti?

ODGOVOR
Ali se lahko domisliš še kakšne zanimive zgodbe, ki bi nazorno ponazorila hitro rast eksponentne funkcije? Pomisli, npr. koliko prednikov bi imel v času, ko je bila zgrajena arena v Puli (pred približno 2000 leti – glej ), če si med njimi nobena dva iz iste generacije ne bi bila v sorodu?

ODGOVOR
Oceni, koliko riža potrebujemo, da pokrijemo cel svet (vključno z oceani), če meri polmer zemlje 6400 km?

ODGOVOR
Če predpostavimo, da je zrno riža v povprečju dolgo 6.4 milimetra in široko 1 milimeter lahko izračunamo površino enega zrna riža, ki je 0.064 cm². Zdaj lahko samo še delimo površino Zemlje s površino riža in dobimo rezultat ki je približno 8*10¹⁹.
Oceni, koliko besed lahko “obdela” tvoj ali pa šolski PC v eni uri? Kolikšna je velikost največjega števila, ki bi ga še lahko zapisal v spomin svojega ali šolskega računalnika?

ODGOVOR
Če procesor deluje s frekvenco 4GHz, to pomeni, da izvede 4*10⁹ cikov na sekundo. Če za eno besedo porabi 10 ciklov, v času 1 ure (3600 sekund) izvede 1.44*10¹³ ciklov in obdela 1.44*10¹² besed.

Največje število, ki ga lahko zapišemo v pomnilnik velikosti 16 Gib (2³⁷ b) v nepredznačenem celoštevilskem zapisu je 2^{1374389534712} -1.
Kolikšna je dolžina produkta dveh binarnih števil, katerih zapisa sta dolga $m$ in $n$?

ODGOVOR
Za množenje binarnih števil velja, da število $a$ dolžine $m$ zadošča sledečemu pogoju: $2^{m-1} \leq a < 2^{m}$. Če ima torej $a_1$ dolžino $m$ in $a_2$ dolžino $n$, lahko zmnožimo neenačbi \[2^{m-1} \leq a_1 < 2^{m}\] \[2^{n-1} \leq a_2 < 2^{n}\] in dobimo $2^{m+n-2} \leq a_1a_2 < 2^{m+n}$, iz katere nato sledi, da je dolžina produkta $a_1$ in $a_2$ enaka vsoti dolžin števil $a_1$ in $a_2$ ali pa je za 1 manjša od te vsote.
Koliko operacij potrebuješ za izračun produkta dveh 100-bitnih binarnih števil s procesorjem/vodilom svojega ali šolskega računalnika?

ODGOVOR
Če je k število bitov, za množenje potrebujemo v grobem $k^2$ operacij, bi lahko naivno rekli da potrebujemo približno $10000$ operacij za izračun. Večina sodobnih računalnikov ima 64-bitno arhitekturo. Torej imajo 64-bitne registre, kar pomeni, da lahko naenkrat računajo le z 64-bitnimi števili. Če želimo zmnožiti 100-bitni števili $a$ in $b$, ju moramo razdeliti na dve 64-bitni števili. Razdelimo ju tako, da velja: \[a=a_1∗2^{64}+a_0\] \[b=b_1∗2^{64}+b_0\] Tako lahko izračunamo njun zmnožek \[a∗b=\] \[=(a_1∗2^{64}+a_0∗2^0 )(b_1∗2^{64}+b_0∗2^0 )=\] \[=a_1 b_1∗2^{128}+(a_0 b_1+a_1 b_0 )∗2^{64}+a_0 b_0\] Torej potrebujemo štiri množenja 64-bitnih števil in eno seštevanje. \[4∗64^2+1=16385\] Torej za množenje dveh 100-bitnih števil potrebujemo $16385$ operacij.
Pri učinkovitem algoritmu računanja potence $\alpha^n$, $n\in \mathbb{N}$, smo vnaprej izračunali potence $\alpha^2,\alpha^{2^2},\alpha^{2^3},\dots$ Poišči učinkovit algoritem za potenciranje, ki potrebuje bistveno manj spomina.

ODGOVOR
En tak algoritem je znan pod imenom kvadriraj in zmnoži, njegov spomin pa je neodvisen od števila $n$.
Poišči čim več parov funkcij, za katere velja pravilo o zamenjavi. Ali znaš s takim parom sestaviti digitalno različico protokola Massey-Omura, ki bo varna?

ODGOVOR
Nekaj parov funkcij, za katere velja pravilo o zamenjavi: \[\begin{array}{|c|c|} \hline \text{Funkcija} & \text{Inverz} & \text{Pogoji} \\ \hline f(x)=x+k & f^{−1}(y)=y−k & \\ \hline f(x)=k−x & f^{−1}(y)=k−y & \\ \hline f(x)=kx & f^{−1}(y)=\frac{y}{k} & \text{Če } k≠0 \\ \hline f(x)=x^k & f^{−1}(y)=\sqrt[k]{y} & \text{Za } x, y≥0 \\ \hline f(x)=k^x & f^{−1}(y)=log_k⁡y & \text{Za } y, k>0 \\ \hline f(x)=1/x & f^{−1}(y)=\frac{1}{y} & \text{ Za } x, y≠0 \\ \hline f(x)=x⊕k &f^{−1} (y)=y⊕k & \\ \hline f(x)=x^e \bmod n & f^{−1} (y)=y^d \bmod n & \text{Če } de \bmod (ϕ(n))=1 \\ \hline \end{array}\]
Ni se težko prepričati, da je ciklična grupa z $n$ elementi izomorfna grupi $(\mathbb{Z}_n,+_n)$. Kaj lahko poveš o relaciji med zahtevnostjo problema diskretnega logaritma v poljubni ciklični grupi $G$ z $n$ elementi in problema iskanja izomorfizma med grupo $G$ in aditivno grupo $(\mathbb{Z}_n,+)$? Opiši napad aktivnega srednjega napadalca za primer protokola Massey-Omura.

ODGOVOR
Imamo grupi $(G, ∗)$ in $(H, ⊙)$. Izomorfizem je taka bijektivna funkcija $f$, ki slika iz $G$ v $H$, da velja: \[f(u∗v)=f(u)⊙f(v)\] Če obstaja izomorfizem iz ene v drugo grupo, pomeni da sta grupi izomorfni. Vsak element v ciklični grupi $C_n$ lahko zapišemo kot $α^i$, če je $α$ generator te grupe in $0<i<n$. Če se želimo pokazati, če je ciklična grupa $(C_n, ∘)$ izomorfna grupi $(\mathbb{Z}_n, +)$ moramo najti bijektivno funkcijo $f$, ki slika iz $C_n$ v $\mathbb{Z}_n$, da velja: \[f(u∘v)=f(u)+f(v)\] Ena takih funkcij je logaritemska funkcija. Prepričajmo se da to drži. \[log_α⁡(α^{i}∘α^{j})=log_α⁡(α^{i})+log_α⁡(α^{j})\] Vemo, da je njen inverz eksponentna funkcija, njeno definicijsko območje je $\mathbb{Z}^+$, slika pa $\mathbb{Z}$, kar pokrije območje obeh grup. To pomeni, da je ta funkcija biektivna. Torej je $log_α⁡(x)$ izomorfizem grup $(C_n, ∘)$ in $(\mathbb{Z}_n, +)$. V Zn velja $log_α⁡(x)=xα^{−1} \bmod n$, kjer je α nek generator grupe $(Z_n, +)$. Tako lahko diskreten logaritem poiščemo na učinkovit način, saj lahko $α^{−1}$ izračunamo z razširjenim evklidovim algoritmom. Za splošno ciklično pa učinkovitega algoritma za reševanje problema diskretnega logaritma zaenkrat še ne poznamo.

7.2 Poštni nabiralnik in kriptografski protokoli

Nadaljujemo zgodbo o dveh vizionarjih Whitfieldu Diffieju in Martinu Hellmanu, ki sta razmišljala o bližajoči se digitalni dobi in odkrila (DH-)dogovor o tajnem ključu (prav neverjetno, a ta ostane tak celo ob nenehni navzočnosti ostrih ušes vohunov). Na srečo se nista ustavila pri tem. Prav nasprotno! Prepričana sta bila, da sta na pravi poti in to jima je dalo svež zagon, ki je bil še kako dobrodošel pri novih odkritjih. Leta 1976 so Whitfield Diffie, Martin Hellman in Ralph Merkle vpeljali revolucionaren koncept kriptosistemov z javnimi ključi, ki ga bomo predstavili v tem razdelku. Ideja je v resnici zelo enostavna, dostopna celo osnovnošolcem, če le nanjo pogledamo iz pravega zornega kota.

Vsakdo, ki ve, kje je nabiralnik, lahko vanj vrže pošiljko, ne more pa je vzeti ven – to lahko stori le tisti, ki ima ključ od nabiralnika.

Nabiralnikov seveda ne skrivamo. Prav nasprotno, običajno so označeni z imenom lastnika in se nahajajo poleg vhoda v blok ali hišo. Večino naslovov prebivalcev lahko najdemo kar v telefonskem imeniku. Zato pravimo, da je taka informacija javna.

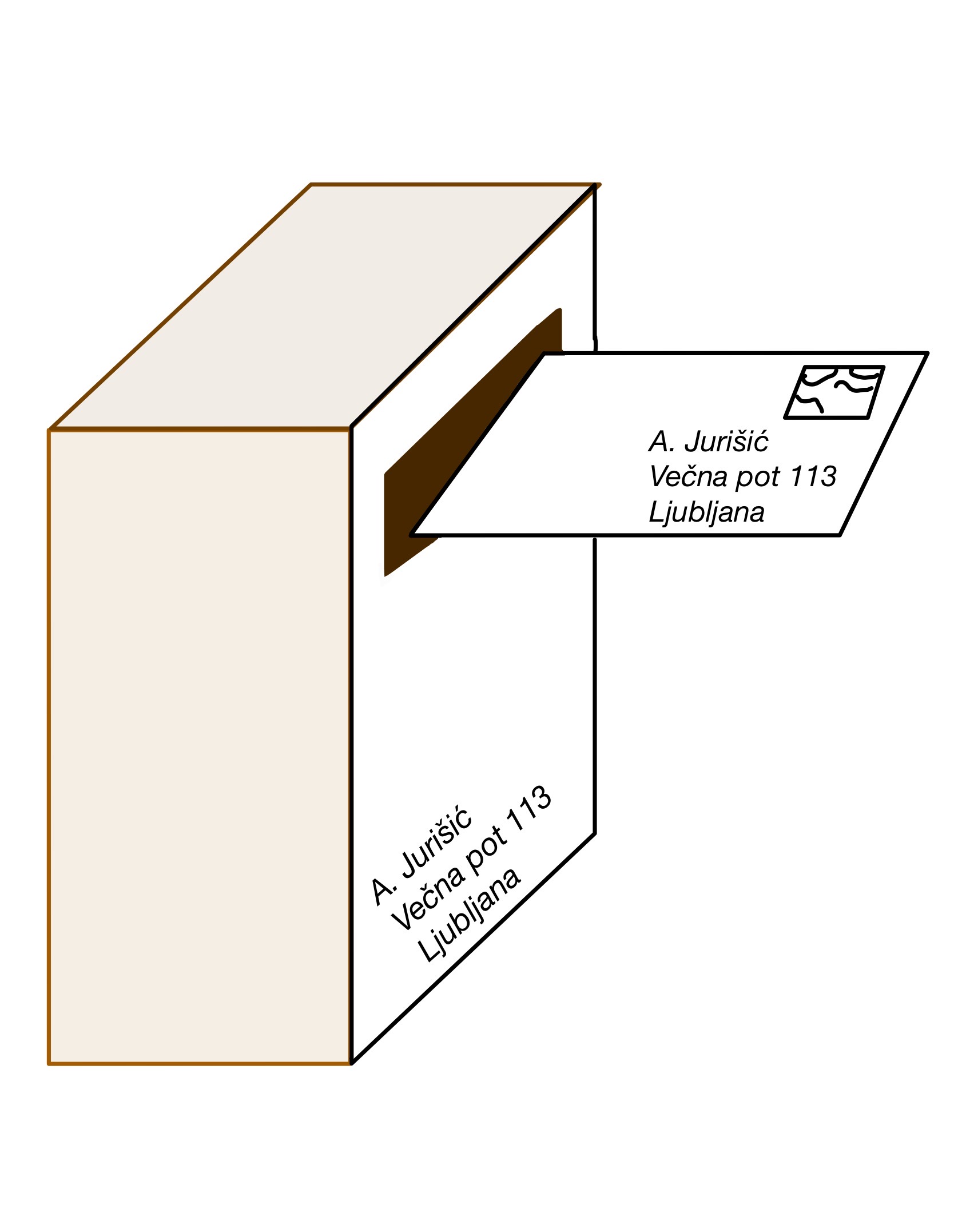
Slika 1. Javno dostopni nabiralnik, ki ga lahko nenasilno odpremo samo z zasebnim ključem.

V nasprotju z zasebnimi oziroma simetričnimi kriptosistemi, v katerih se uporablja en sam ključ za šifriranje čistopisa in odšifriranje tajnopisa, ima pri kriptosistemih z javnimi ključi vsak uporabnik (to je lahko tudi naprava, npr. tiskalnik) svoj par ključev:

zasebnega, tj. v našem primeru ključ od nabiralnika, in
javnega, tj. informacijo o tem, kam je postavljen ustrezni nabiralnik oziroma kako je označen (če moramo izbrati med številnimi, na videz enakimi, nabiralniki).

Zato takim sistemom rečemo tudi asimetrični kriptosistemi.

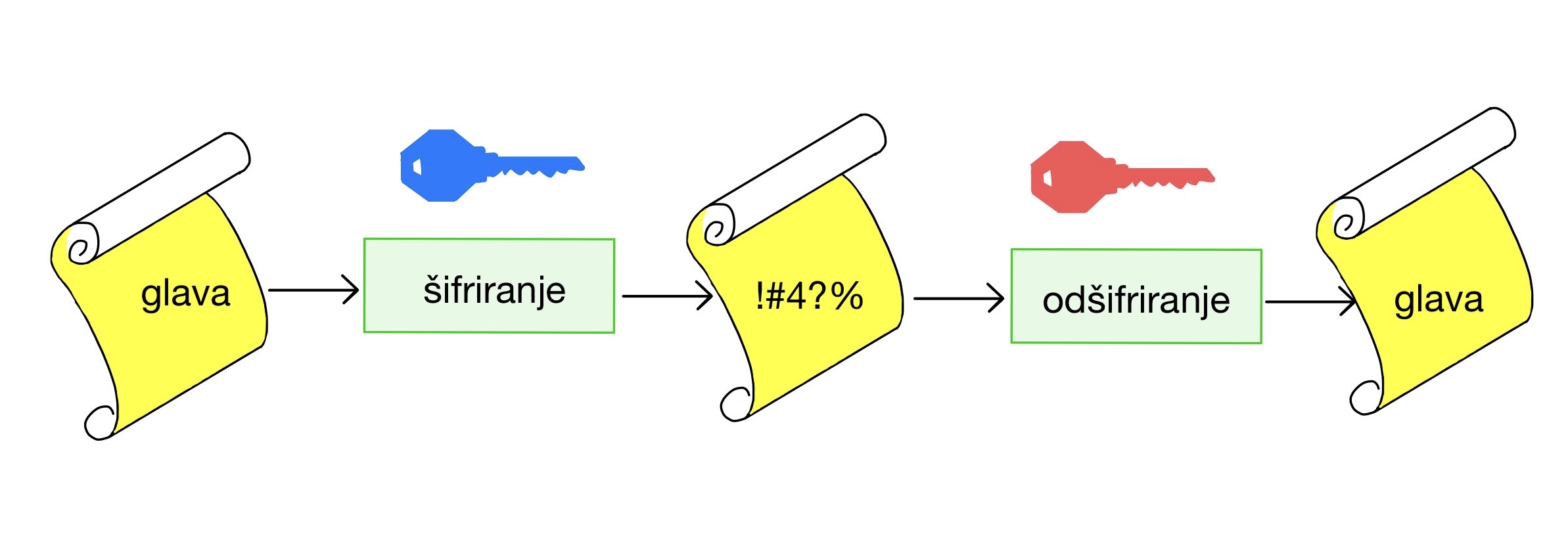
Slika 2. Asimetrični kriptosistem uporablja javni ključ za šifriranje in zasebni za odšifriranje. Uporabnik najprej objavi svoj javni ključ, zasebnega pa spravi na varno. Nato lahko vsakdo z javnim ključem zašifrira pismo, bral oziroma odšifriral pa ga bo lahko le lastnik ustreznega zasebnega ključa.

Asimetrični kriptosistem uporablja javni ključ za šifriranje in zasebni za odšifriranje. Uporabnik najprej objavi svoj javni ključ, zasebnega pa spravi na varno. Nato lahko vsakdo z javnim ključem zašifrira pismo, bral oziroma odšifriral pa ga bo lahko le lastnik ustreznega zasebnega ključa.

Če se torej Anita in Bojan želita varno pogovarjati, objavita svoja javna ključa, zasebna pa zadržita zase. Ko želi Anita poslati zaupno sporočilo Bojanu, ga z njegovim javnim ključem zašifrira (tj. vrže pismo v Bojanov nabiralnik), Bojan pa je edini, ki pozna odšifrirni (zasebni) ključ in lahko dobljeno sporočilo odšifrira ter prebere. En ključ podatke zaklepa, drugi pa jih odklepa.

Pomembna lastnost tega sistema je, da ključ, ki zaklepa, ne more odklepati in obratno, ključ, ki odklepa, ne more zaklepati.

Bolj natančno pa bomo rekli, da se iz javnega ključa ne da učinkovito (to pomeni v doglednem času, za katerega želimo zadržati napadalca) izračunati zasebnega ključa. Tako lastnik en ključ objavi, drugega pa hrani na varnem (npr. na pametni kartici, ki jo nosimo že v vsakem mobilnem telefonu). To omogoča ljudem varno komuniciranje, ne da bi se predhodno srečali zaradi izmenjave oziroma dogovora o tajnem ključu.

Ideja kriptosistema z javnimi kjuči

Kriptosistem z javnimi ključi bomo opisali v treh enostavnih korakih:

Ko Anita objavi svoj javni ključ in Bojan z njim zašifrira pismo, namenjeno Aniti, lahko le ona odšifrira to pismo. Tako dosežemo zasebnost.
Vlogo ključev lahko tudi zamenjamo in dobimo digitalni podpis: če Bojan najprej zašifrira pismo z zasebnim ključem (tj. ga digitalno podpiše), lahko vsakdo, ki dobi tajnopis, prebere (odšifrira) zašifrirano pismo, nihče pa ne more ponarediti podpisa, saj ima le Bojan zasebni (šifrirni) ključ. S tem dosežemo pristnost Bojanovega pisma.

Sedaj pa združimo zasebnost in pristnost.

Če želi Bojan poslati Aniti podpisano zasebno pismo (glej sliko 3), ga najprej zašifrira s svojim zasebnim ključem $Z_B$ (ga podpiše), nato si priskrbi Anitin (šifrirni) javni ključ $J_A$, z njim zašifrira že podpisano pismo in ji le-to pošlje. Anita prejeto pošiljko najprej odšifrira s svojim zasebnim ključem $Z_A$. Nato si priskrbi Bojanov javni ključ $J_B$ ter z njim preveri podpis, tj. z Bojanovim javnim ključem odšifrira zašifrirano pismo ter se prepriča, da ji ga je res poslal Bojan.

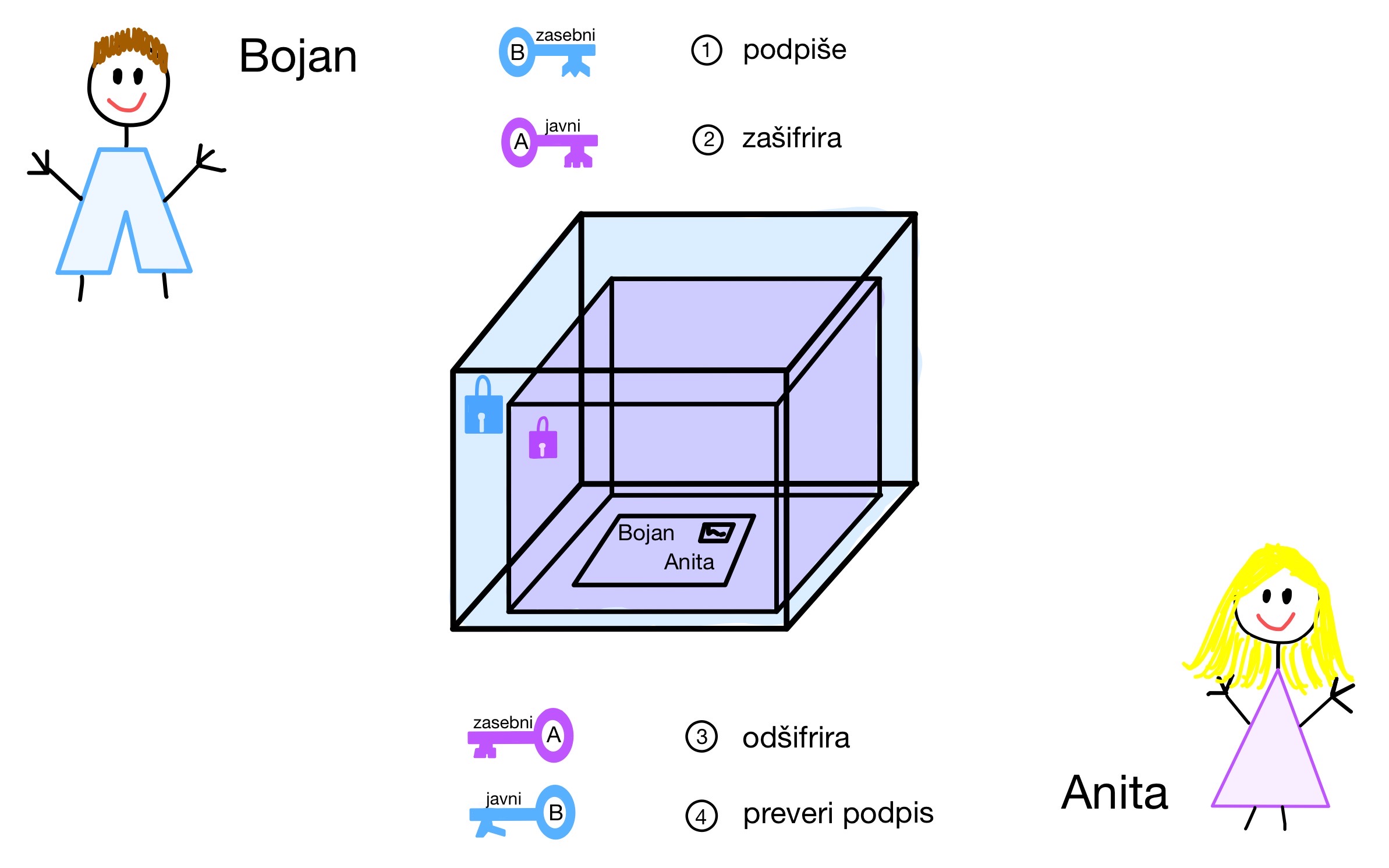
Slika 3. V točki (c) smo združili zasebnost in pristnost. Namesto operacij šifriranja in odšifriranja si je morda lažje predstavljati konkretne modele. V ta namen vidimo zgoraj dve škatli s ključavnicama.
Za črno ključavnico lahko uporabljamo le črna ključa (Bojanov zasebni in javni ključ), za belo pa le bela (Anitin zasebni in javni ključ).

Ideja je sedaj na mizi, nas pa zanima njena konkretna digitalna izvedba, saj ne želimo biti odvisni od (ne)varnih škatel, kaj šele od fizičnih ključavnic in ključavničarjev.

Kakšno zagotovilo dobimo, da je daljinski ključ za odpiranje garažnih vrat ali parkirišča zares varen? V resnici prav nobenega! Prodajalec nam morda še zna na začetku zamomljati, da gre pri ključavnici za milijone kombinacij. Ko pa mu osnovnošolec odvrne, da to ni prav dosti za današnje računalnike (na običajnem PC-ju lahko preverimo 30 milijonov gesel na sekundo), je zagotovil hitro konec. No, morda nas usmerijo le še na tujega dobavitelja, od katerega pa seveda nikoli ne dobimo jasnih odgovorov.

Se spomnite, da smo tudi v drugem delu [2] omenjali ključavnice (protokol Massey-Omura)? Povedali smo, da jih lahko v digitalnem svetu zamenjamo s parom obrnljivih funkcij, ki med seboj komutirata (tj. zanje velja pravilo o zamenjavi). V istem sestavku smo v deveti nalogi povprašali po takih funkcijah. Ni jih težko najti, saj nas že prištevanje skrivnih števil reši iz zagate. Če tajnemu ključu $K$ Anita prišteje svoje skrivno število a in nato prišteje svoje skrivno število b še Bojan, jih lahko v istem vrstnem redu še odštejeta in tako pride Bojan do ključa K. Po javnem kanalu pa so zaporedoma potovali le števila $K+a$, $K+a+b$ in $K+b$, torej nikoli tajni ključ $K$. Seveda je v tem primeru dobro uporabiti modularno seštevanje (ni pa nujno). Še vedno dovolj učinkovito je tudi množenje s skrivnimi števili, za računalnike pa je še najbolj primerna operacija ekskluzivni ali (XOR). Vse te funkcije pa ne nudijo dejanske varnosti, saj lahko napadalec izračuna ključ iz znanih količin, npr. $K+b-[(K+a+b)-(K+a)]=K$. Ugotovili smo torej, da učinkovitost ni edini kriterij za take funkcije, saj moramo zagotoviti še, da obratna operacija nima te lastnosti.

Enosmerne funkcije so tiste, ki jih znamo zlahka izračunati (tj. z učinkovitim algoritmom), računanje v obratni smeri pa je težko (ne nujno vedno, v povprečju pa pravgotovo). Morda boste pomislili, da je že množenje s konstanto primer take funkcije, a za računalnike množenje ni kaj dosti bolj počasno (v primeru modularnega množenja to opravimo z razširenjim Evklidovim algoritmom, glej [3]). Tudi funkcijo $f(x)=x^2$ znamo hitro izračunati, vendar pa le-ta še ni prava kandidatka, saj se da relativno hitro izračunati tudi kvadratni koren.

Matematiki in računalnikarji si še vedno niso na jasnem, ali enosmerne funkcije sploh obstajajo. To je eden izmed slovitih odprtih problemov. Obstoj takšnih funkcij ima številne zanimive posledice (za starejše bralce omenimo npr. posledico $P\ne NP$).

Funkcije, ki so jih iskali na začetku omenjeni kriptografi, bi naj bile obrnljive le s pomočjo neke skrivnosti (angl. trap-door one-way functions). Npr. če razstavimo zapleteno napravo, jo je zelo težko sestaviti brez načrta, medtem ko z načrtom še nekako gre. Matematični primer pa bi bilo množenje dveh velikih praštevil, ki ga znamo hitro opraviti. Za dan produkt dveh praštevil je tudi preverjanje, ali sta dani praštevili tisti, ki nam dasta pravi produkt, zelo učinkovito. Za dan produkt brez poznavanja praštevil pa je izredno težko najti faktorje.

V razvoju kriptografije z javnimi ključi je bilo predlaganih in razbitih veliko kriptosistemov. Le nekaj jih je prestalo časovni test varnosti in jih lahko danes smatramo za razmeroma varne in učinkovite. Glede na matematični problem, na katerem temeljijo, so razdeljeni v tri skupine:

sistemi faktorizacije celih števil, npr. RSA (Rivest-Shamir-Adleman), glej [4];
sistemi diskretnega logaritma, npr. ElGamal in DSA;
kriptosistemi z eliptičnimi krivuljami (Elliptic Curve Cryptosystems).

Prvi konkreten model kriptosistema z javnimi ključi so prelagali že leta 1977 Ronald Rivest, Adi Shamir in Leonard Adleman. Na drugega je bilo potrebno počakati skoraj celo desetletje (1985) in ga bomo predstavili v 4. delu, tretjega pa sta predlagala neodvisno Victor Miller (1986) in Neal Koblitz (1987).

Protokoli v kriptografiji

Protokol ni samo nekaj, kar morajo obvladati politiki, pač pa postopek, po katerem opravimo določen pogovor/komunikacijo. Za primer si oglejmo protokol, ki ga moramo poznati, če želimo obiskati učiteljico v njenem kabinetu.

Najprej se pozanimamo, kje je njen kabinet in kdaj ima govorilne ure. Nato odidemo tja ob pravem času. Ko želimo vstopiti, najprej potrkamo, počakamo na povabilo (Naprej!), nato odpremo vrata, pozdravimo in običajno še zapremo vrata. (Tudi če ne dobimo vabila, marsikoga zamika, da bi vseeno pritisnil na kljuko, pa čeprav to ni dovoljeno.)

Tak protokol za vstop v pisarno bi v šoli na zavodu za gluhoneme otroke izgledal povsem drugače. Učenec ne bi mogel slišati povabila, morebitni gluhi učitelj ne bi slišal trkanja, nemi pa bi ga moral povabiti naprej na kakšen drug način. Privzeli smo tudi, da poteka protokol v varnem okolju. Če pa temu ni tako, mora biti protokol seveda precej drugačen, glej zgodbo o volku in sedmih kozličkih ali pa se spomni na mrke redarje, ki pogledajo čez majhno lino v vratih.

Opozoriti velja, da majhna sprememba v protokolu lahko kaj hitro pomeni veliko luknjo za varnost. Tudi računalniki in uporabniki na internetu se morajo držati pravil in s tem zagoto- viti vse elemente varnosti, kot so zasebnost, celovitost (tj. zaščita pred spremembo vsebine), pristnost. Temu pravimo kriptografski protokol. Dokazati varnost nekega kriptografskega protokola je sila zahtevna naloga. Pogosto je mnogo lažje najti kakšen učinkovit napad (če seveda obstaja).

Za konec pa se vživimo še v en pravljični protokol, ki ga vsi dobro poznamo. Se še spomnite pravljice o lačnem volku in sedmih kozličkih?

Volk in sedem kozličkov (brata Grimm).

Nekoč je živela stara koza, ki je imela sedem kozličkov. Nekega dne se je odpravila v gozd po krmo, še prej pa je sklicala vseh sedem otrok in jim rekla:

“Ljubi otroci, v gozd grem, vi pa se varujte volka! Če bi prišel noter, bi vas požrl s kožo in kostmi. Grdavš se velikokrat pretvarja, da je kdo drug, toda takoj ga boste prepoznali po njegovem hripavem glasu in črnih tacah.”

“Ljuba mama, zelo bomo pazili nase, kar brez skrbi pojdi,” so rekli kozlički.

Koza je zameketala in pomirjena odšla na pot. Nedolgo zatem je potrkalo na vrata hišice in nekdo je zaklical:

“Odprite, otročički, vaša mama trka in vsakemu je nekaj prinesla.”

Toda kozlički so slišali hripavi glas in so takoj vedeli, da je volk. Zaklicali so:

“Ne odpremo ti! Ti že nisi naša mama. Naša mama ima nežen in ljubezniv glas, tvoj pa je hripav! Ti si volk!”

Volk je takoj odšel k trgovcu in si kupil velik kos krede. Pojedel jo je in njegov glas je postal nežnejši. Potem je šel nazaj, še enkrat potrkal na vrata hišice in zaklical:

“Odprite, otročički, vaša mama trka in vsakemu je nekaj prinesla.”

Toda kozlički so videli volkovo črno taco na oknu in so zaklicali:

“Ne odpremo ti! Naša mama nima takih črnih tac kot ti. Ti si volk!”

Zdaj je volk stekel k peku in mu rekel:

“Udaril sem se v taco, pomaži mi jo s testom!!”

Ko mu je pek pomazal taco s testom, je stekel še k mlinarju in mu rekel:

“Posuj mi taco z belo moko!”

Mlinar si je misli: “Tale volk bo gotovo nekoga osleparil,” in ni hotel narediti tega.

“Požrl te bom!”

je zarjul volk in mlinar se je ustrašil in mu ustregel. Takšni so pač ljudje.

Zdaj je šel hudobnež že tretjič do hišice, potrkal je in rekel:

“Odprite otročički, vaša ljuba mamica je prišla domov in vsakemu nekaj prinesla iz gozda.”

Kozlički so zaklicali:

“Najprej nam pokaži taco, da bomo res vedeli, ali si naša ljuba mamica.”
Volk je položil taco na okno, in ko so kozlički videli, da je bela, so mu verjeli …

Naloge

Konkreten model kriptosistema z javnimi ključi predstavlja dobro znani kriptosistem RSA. Preuči ga, nato ga implementiraj za kakšne male vrednosti in končno predlagaj prijatelju, da najde kakšno šibko točko. Če mu uspe, slabost odpravi in ga zopet pozovi k napadanju. To ponavljajta nekaj časa, potem pa vlogi zamenjajta. Običajno je taka igra zelo podobna tudi “tekmi” med kriptografi in kriptoanalisti.
Ponovi prejšno nalogo še za kakšen kriptosistem z javnimi ključi (npr. tistega, ki uporablja metodo nahrbtnika).
Opiši kakšno pomanjkljivost protokola Massey-Omura. Nato pa poišči kakšno lastnost funkcij, s katerimi izvedeš ta protokol, ki bo to pomanjkljivost odpravila.
Bilo je temno kot v rogu, ko se je vohun vračal v grad po opravljeni akciji v sovražnem taboru. Ko se je približal vratom, je zaslišal šepetajoč glas: “Geslo ali streljam!” Kako lahko vohun prepriča “stražarja”, da pozna geslo, ne da bi ga izdal morebitnemu vsiljivcu/prisluškovalcu?

Slika

Predlagaj čimveč enosmernih funkcij. Zopet lahko organiziraš tekmo med kriptografi (sestavljalci šifer) in kriptoanalisti (razbijalci šifer).
Predlagaj kakšno enosmerno funkcijo, ki je obrnljiva s pomočjo neke skrivnosti (tu bi morala biti tekma med kriptografi in kriptoanalisti morda še bolj zanimiva).

Viri in dodatno branje

[1] A. Jurišić in Urban Perko, Klasične šifre in zdravstvena kartica, Presek 33/1 (2005-06), str. 22-24.

[2] A. Jurišić, Diffie-Hellmanov dogovor o ključu, Presek 34 (2006-07), str. 25-30.

[3] M. Juvan, O Evklidovem algoritmu, Presek 21 (1993-94), str. 116-121.

[4] M. Vencelj, Šifriranje z javnim ključem, Presek 22/6 (1994-05), str. 354-357.

7.3 Zaupati ali ne zaupati (digitalni podpisi)

Pred petdesetimi leti je imel le malokdo doma telefon, danes pa redkokateri učenec med poukom ne pogleda s svojim mobilcem na Internet (npr. Facebook). Tako se nam vsaj navidezno zdi, da smo obkroženi s “stevilnimi prijatelji. Pa vendar so ljudje že davno prišli do zaključka, da so človeški možgani sposobni res dobro razumeti največ 150 posameznikov in odnosov med njimi (npr. Robin Dunbar iz univerze v Liverpoolu). Tudi v podjetjih in vojski se število 150 izkaže za kritično, kadar je obravnavana najmanjšo neodvisno enoto. Kadar se npr. z neko disciplino ukvarja več kot 200 raziskovalcev, se običajno le-ta razcepi na dve ali več podpodročij. V vaseh, ki štejejo čez 500 prebivalcev, se torej že pojavlja anonimnost, da o večjih mestih niti ne govorimo. V današnjem času interneta in potrošniške družbe bo zato vse pogosteje prihajalo do komuniciranja med ljudmi (celo med napravami), ki se ne poznajo. Kako si torej lahko zaupata dva, ki sta se začela pogovarjati preko mreže?

V tretjem razdelku smo predstavili koncept kriptosistemov z javnimi ključi, ki so ga leta 1976 odkrili W. Diffie, M. Hellman in R. Merkle (zadnji je bil takrat še študent), in tudi idejo digitalnega podpisa. V tem sestavku bomo predstavili konkreten kriptografski protokol, ki omenjeno idejo uvaja v prakso. Po razmisleku o lastnostih lastnoročnega in digitalnega podpisa bomo opisali Elgamalovo shemo za digitalni podpis, ki je poleg RSA sheme [5]

V bistvu se način zapisovanja informacij ni drastično spremenil. Medtem ko smo prej shranjevali in prenašali informacije na papirju, jih sedaj hranimo na diskih in v drugih elektronskih/magnetnih medijih ter jih prenašamo preko omrežij. Bistveno pa se je spremenila možnost kopiranja, prenašanja in spreminjanja informacij. Zlahka naredimo na tisoče kopij neke digitalne informacije in jih v trenutku spravimo na različne konce sveta, pri tem pa se nobena kopija prav nič ne razlikuje od originala. Z informacijo na papirju je bilo vse to precej težje, če že ne nemogoče. Poskrbeti moramo, da bo varnost informacij neodvisna od fizičnega medija, ki jih je zapisal ali prenesel. Temeljiti mora izključno na digitalni vsebini, tj. številkah. Zato zna biti današnja tema zanimiva tudi za nas, Presekovce.

Eno izmed osrednjih orodij za zaščito informacij je podpis. Le-ta preprečuje poneverjanje in je dokaz o izvoru, identifikaciji, pričanju. Podpis naj bi bil unikat vsakega posameznika, saj se z njim predstavljamo, nekaj potrjujemo, nekoga pooblaščamo,…

Slika

Z digitalnim podpisom potrjujemo izvor podatkov ali pa nekoga prepričamo, da je podpis opravil lastnik ustreznega zasebnega ključa.

Z razvojem digitalne informacije moramo ponovno obdelati bistvo podpisa. S pravo idejo lahko vplivamo na tok zgodovine, saj ni rečeno, da ne bi mogli dodati še kakšne nove lastnosti, na katero doslej še nihče ni pomislil, le-ta pa bi lahko nam vsem spremenila življenja oziroma vsaj navade.

(Stari) lastnoročni podpis

Na podiplomskem študiju mi je moral mentor na začetku vsakega semestra podpisati formular, na katerem so bili vpisani predmeti, ki sem si jih izbral za tisti semester. Ko sem že dobil podpis, sem na seznamu sosednjega oddelka za računalništvo zagledal še dva zanimiva predmeta. Opazil sem, da je v formularju prostor ravno še zanju in ju vpisal. Pa vendar sem pomislil tudi na to, da tak način morda ni ustrezen in sem mentorja obvestil o spremembi. Izkazalo se je, da bi ga moral v resnici še enkrat prositi za odobritev, ne pa samo obvestiti. In zato ni bil nič kaj zadovoljen, da sploh lahko pride do takšnih zapletov. Kakšno leto kasneje sem izvedel, da mentorji dobijo kopije študentskih formularjev neposredno iz pisarne, kamor smo jih oddajali.

Pogled v bližnjo prihodnjost nam razkrije še nekaj pomanjkljivosti lastnoročnega podpisovanja:

J. “Danes sem dobil podpis v šoli,” pove Janezek sestri.
S. “Kakšno neumnost si pa zopet naredil?”
J. “Te nič ne briga, raje mi svetuj, kako naj prelisičim mamo.”
S. “Nad učiteljev podpis skopiraj obvestilo o športnem dnevu.”
J. “Odlična ideja, na ta način se bom zlahka rešil zagate, pa še smučat grem, namesto da bi šel v šolo.”

Slika

Janezek to naredi in mama pod digitalno obvestilo o smučarskem dnevu pripne svoj “digitalni” podpis. Preden pa ga Janezek na ključku odnese v šolo, zopet zamenja obvestilo o športnem dnevu s prejšnjim tekstom. V resnici je škoda za starše še večja, saj ima sedaj Janezek mamin “digitalni” podpis in ga bo odslej lahko izrabljal po mili volji. V času elektronskih medijev je zato izredno nevarno podpis skenirati (posneti) oziroma sprejemati skenirane podpise, ki so v resnici le posnetki. Postopek digitalnega podpisa mora biti dobro premišljen, saj moramo preprečiti spreminjanje vsebine podpisanega sporočila in ponarejanje oziroma kopiranje podpisa. Zgoraj opisani digitalni podpis ni več unikat, ki enolično določa podpisnika. Z lahkoto ga kopiramo oziroma dodamo na poljuben dokument. Potrebujemo protokole, ki imajo podobne lastnosti kot trenutni “papirni protokoli”. Današnja družba ima enkratno priložnost, da vpelje nove in še učinkovitejše načine, ki nam bodo zagotovili boljšo varnost informacij.

Digitalni podpis naj bi bil nadomestek za lastnoročni podpis pri elektronski izmenjavi in digitalnemu hranjenju podatkov. Nastopa kot število oziroma še bolj splošno kot zaporedje bitov.

Digitalni podpis mora imeti vse dobre lastnosti, ki veljajo za lastnoročni podpis, poleg tega pa mora veljati, da vsebine digitalno podpisanega dokumenta ni mogoče spreminjati in podpisa ni mogoče kopirati in ponarejati. Obe obliki podpisovanja pa imata še nekaj pomembnih lastnosti:

Lastnoročni podpis je fizično del podpisanega dokumenta.
Lastnoročni podpis preverjamo s primerjanjem, digitalnega pa z algoritmom, ki ga izvaja računalnik. Rezultat tega preverjanja je odvisen od ključa ter dokumenta, ki smo ga podpisali.
Digitalnega podpisa ne moremo razlikovati od njegove kopije, zato si želimo podpis, ki bo vedno drugačen (četudi podpišemo isto stvar).

Povedali smo že, da je digitalni podpis odvisen od dokumenta, ki ga podpisujemo. Ker pa so dokumenti poljubno veliki, običajno iz dokumenta skonstruiramo izvleček fiksne dolžine (lahko bi mu rekli tudi prstni odtis) in nato podpišemo le-tega. Tokrat se ne bomo spuščali v podrobnosti teh postopkov, ki jim rečemo {}, pač pa omenimo le, da je mogoče priti do izvlečka z bločnimi simetričnimi šiframi, ki smo jih spoznali v prvem delu [1], glej 2. in 3. nalogo.

Slika

(Novi) digitalni podpis

Shema za digitalni podpis je sestavljena iz treh delov:

iz algoritma za generiranje ključa,
algoritma za generiranje digitalnega podpisa in
algoritma za preverjanje digitalnega podpisa.

Za lažje razumevanje definirajmo nekaj osnovnih pojmov.

Pravilo ${\tt sig}_{Z(A)}$, ki sporočilo podpiše (angl. sign), imenujemo osebe $A$. Zasebni ključ $Z(A)$ varuje oseba $A$ in ga uporablja le za podpisovanje dokumentov.
Pravilu ${\tt ver}_{J(A)}$, ki za dokument in njegov podpis preveri oz. verificira (angl. verify), tj. priredi vrednost “veljaven” oziroma “neveljaven”, rečemo osebe $A$. Javni ključ $J(A)$ pripada osebi $A$, a je vseeno javno znan. “Tretja” oseba uporablja ${\tt ver}_{J(A)}$ za preverjanje podpisov, ki jih je opravila oseba $A$.

Postopek pošiljanja digitalno podpisanega sporočila med Anito in Bojanom je naslednji:

Najprej si Bojan izbere svoj zasebni ključ $Z(B)$ ter sporoči Aniti ustrezni javni ključ $J(B)$.
Za podpis sporočila $x$, Bojan uporabi algoritem za generiranje digitalnega podpisa s svojim zasebnim ključem $Z(B)$ in izračuna podpis ${\tt sig}_{Z(B)}(x)$. Nato ga skupaj s sporočilom pošlje Aniti.
“Ce Anita pozna Bojanov javni ključ $J(B)$, lahko uporabi algoritem za preverjanje digitalnega podpisa ${\tt ver}_{J(B)}$ ter tako preveri pristnost podpisa.

Vrstni red šifriranja in digitalnega podpisovanja je pomemben.

Če hoče Anita poslati Bojanu podpisano, zašifrirano sporočilo, potem danemu čistopisu $x$ najprej izračuna svoj podpis $y={\tt sig}_{Z(A)}(x)$, nato zašifrira $x$ in $y$ z Bojanovo javno šifrirno funkcijo $e_{J(B)}$ in dobi $z=e_{J(B)}(x,\, y)$. Tajnopis $z$ pošlje Bojanu. Ta ga odšifrira s svojo zasebno odšifrirno funkcijo $d_{Z(B)}$ in dobi par $(x,\, y)$. Potem uporabi Anitino javno funkcijo ${\tt ver}_{J(A)}$, da preveri, ali je ${\tt ver}_{J(A)}(x,\, y)={\rm veljaven}$.
Če pa bi Anita najprej zašifrirala sporočilo $x$ in potem podpisala rezultat, bi izračunala $z=e_{J(B)}(x)$ in $y={\tt sig}_{Z(A)}(z)$ ter par $(z,\, y)$ poslala Bojanu. Bojan bi z odšifriranjem tajnopisa $z$ dobil $x=d_{Z(B)}(y)$, nato bi preveril podpis $y$ na $x$ z uporabo funkcije ${\tt ver}_{J(A)}$. Če prestreže takšen par $(z,\,y)$ Oskar, nastane problem, saj lahko zamenja Anitin podpis s svojim $y'={\tt sig}_{Z(O)}(z)$, čeprav ne pozna čistopisa $x$. Ko pošlje par $(z,\, y')$ Bojanu, bi ta lahko mislil, da mu je sporočilo $x$ poslal Oskar.

Zato priporočamo najprej podpisovanje in nato šifriranje sporočil, glej 4. nalogo.

Če veljata naslednji dve lastnosti:

Anita je edina, ki lahko podpiše sporočilo, torej edina, ki zna pri danem $x$ izračunati $y$, tako da je ${\tt ver}_{Z(A)}(x,\, y)={\rm veljaven}$,
Bojan se je sposoben prepričati, ali gre za Anitin podpis ali pa gre za ponaredek,

potem rečemo, da je algoritem digitalnega podpisa varen. V naslednjem razdelku bomo predstavili konkretne opise funkcij ${\tt sig}$ in ${\tt ver}$, ki ju smatramo za varne.

ElGamalov digitalni podpis

Opišimo Elgamalovo shemo za digitalni podpis (1985), ki temelji na težavnosti problema diskret-nega logaritma (oznaka DLP) v grupi $\mathbb{Z}_p^*$ in Diffie-Hellmanovega dogovora o ključu, ki smo ju opisali v drugem delu [2]. Spomnimo se, da smo za praštevilo $p$ z $\mathbb{Z}_p$ označili obseg z elementi $\{0,1,\dots,p-1\}$ in operacijama $+_p,*_p$, kjer oznaka $p$ pri $+$ in $*$ pomeni, da običajno vsoto oziroma produkt nadomestimo z ustreznim ostankom pri deljenju s $p$. V $\mathbb{Z}_p$ vedno obstaja tak element $\alpha$, ki generira multiplikativno grupo $\mathbb{Z}_p^{*}=(\{1,\dots,p-1\},*_p)$, tj. množica $\{\alpha^0,\alpha^1,\dots,\alpha^{p-2}\}$ pokrije vse elemente v $\mathbb{Z}_p^{*}$. DLP v $\mathbb{Z}_p^*$ je, da za dani generator $\alpha$ in $\beta=\alpha^a$, kjer je $a$ neko naravno število, iščemo učinkovit način (algoritem) za izračun števila $a$.

Elgamalov algoritem

Priprava: naj bo $p$ tako praštevilo, da je v obsegu $\mathbb{Z}_p$ težko rešiti DLP in $\alpha$ generator grupe $\mathbb{Z}_p^{*}$.
Generiranje ključev: za (skriti) zasebni ključ $a\in \{0,\dots,p-1\}$ izračunaj javni ključ $\beta = \alpha^a \ \mod{p}$.
Podpisovanje: za sporočilo $x\in \{0,\dots,p-2\}$ izberi naključno skrito naravno število $k\le p-2$, tako da je $D(k,p-1)=1$, nato pa z zasebnim ključem $a$ izračunaj ${\tt sig}_a (x, k) = (\gamma, \delta)$, kjer je \[ \gamma =\alpha^k \ \mod{p} \qquad {\rm in} \qquad \delta = (x - a \gamma) k^{-1} \ \mod (p-1). \]
Preverjanje podpisa $(\gamma,\delta)$ sporočila $x$ z javno trojico $(p,\alpha,\beta)$: \[ {\tt ver}_\beta (x, \gamma, \delta) = {\rm veljaven} \ \ \ \Longleftrightarrow\ \ \ \ \beta^{\gamma} \gamma^{\delta} \equiv \alpha^x \pmod{p}. \]

Slika. Taher Elgamal (iz Egipta).

Za pravilnost preverjanja glej 5. nalogo. Zgornji podpis je nedeterminističen (odvisen od naključnega števila $k$), torej sploh ni natanko določen. “Ce torej isti dokument podpišemo vsaj dvakrat, bo z veliko verjetnostjo podpis vsakič drugačen. Poudarimo tudi, da podpisnik izračuna podpis z uporabo tako tajne vrednosti $a$, ki je del ključa, kot tajnega naključnega števila $k$, ki se sme uporabiti samo za podpis {} sporočila $x$ (preverjanje pa je opravljeno samo z uporabo javnih informacij). Če namreč naključno število $k$ ne ostane skrito, ali pa se isto število $k$ uporabi v podpisih dveh različnih sporočil (v tem primeru ga je možno zlahka izračunati), lahko napadalec iz druge enačbe algoritma za podpisovanje izračuna tajno vrednost $a$ in ponaredi podpis. Glej 6. in 7. nalogo. Elgamalovo shemo za podpis smatramo za varno. Do danes namreč še nikomur ni uspelo učinkovito izračunati par $(\gamma, \delta)$ brez računanja diskretnega logaritma. Lahko pa se zgodi, da bomo nekoč ugotovili, da se pri iskanju para $(\gamma, \delta)$ problemu diskretnega logaritma sploh ne moremo izogniti.

$Slika. Pierre de Fermat je poznan tudi po naslednjemu izrek [4]: Za praštevilo p in a \in \mathbb{Z}_p^* velja a^{p-1} \equiv 1 \pmod{p}.$

Slika. Pierre de Fermat je poznan tudi po naslednjemu izrek [4]: Za praštevilo $p$ in $a \in \mathbb{Z}_p^*$ velja $a^{p-1} \equiv 1 \pmod{p}$.

Kako bi lahko ponaredili podpis, ne da bi vedeli za vrednost skritega števila $a$?

Za dano sporočilo $x$ poišči tak par $(\gamma,\delta)$, da bo veljalo $\beta^{\gamma} \gamma^{\delta} \equiv \alpha^x \pmod{p}$:
1. če izberemo $\gamma$, rabimo $\delta = \log_{\gamma} \alpha^x \beta^{-\gamma} \pmod{p}$,
2. če izberemo $\delta$, je potrebno rešiti enačbo $\beta^{\gamma}\gamma^{\delta}\equiv\alpha^x\pmod{p}$ po $\gamma$,
3. hkrati računamo $\gamma$ in $\delta$ (zaenkrat ni še nihče odkril hitrega postopka za reševanje zgornje enačbe).
Za podpis $(\gamma,\delta)$ poišči ustrezno sporočilo $x$, tj. izračunaj: $x = \log_{\alpha} \beta^{\gamma} \gamma^{\delta} \pmod{p}$.

Omenimo še, da so Elgamalov digitalni podpis temeljito preučili tudi v ZDA, kjer na državnem nivoju neradi plačujejo patente (RSA je bil namreč takrat še patentiran). Na njegovi osnovi so sestavili Digital Signature Algorithm (DSA), ki ga je National Institute of Standards and Technology (NIST) sprejel za ameriški standard: Digital Signature Standard (DSS). Danes je vključen v večino varnostnih standardov.

7.3.0.1 Naloge

Viri in dodatno branje

[1] A. Jurišić in U. Perko, Klasične šifre in zdravstvena kartica, 1. del, Presek 33/1 (2005-06), str. 22-24.

[2] A. Jurišić, Diffie-Hellmanov dogovor o ključu, 2. del, Presek 34 (2006-07), str. 25-30.

[3] A. Jurišić, Poštni nabiralnik in kriptografski protokoli, kriptosistemi z javnimi ključi, 3. del, Presek 36/2 (2008-09), 22-26.

[4] D. Pagon, Kongruence in Eulerjev izrek, Presek 15/4 (1987/88), str. 194-196.

[5] M. Vencelj, Šifriranje z javnim ključem, Presek 22/6 (1994-05), str. 354-357.

7.4 Kriptosistemi

Skozi knjigo smo se srečali z veliko simetričnimi kriptosistemi, kot so Cezarjeva šifra, Vigenerjeva šifra, One Time Pad. Pravimo jim simetrični kriptosistemi saj uporabljajo isti skrivni parameter - ključ za kodiranje in dekodiranje.

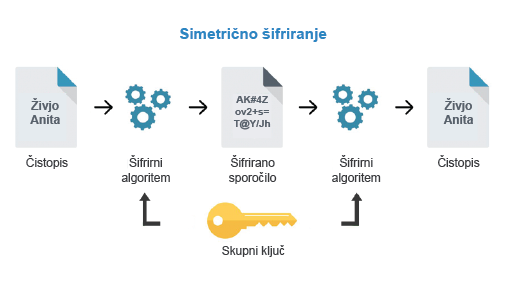
NB. Vzemimo primer da Eve pošlje sporočilo Bobu, oba morata imeti isti ključ da lahko zakodirata in dekodirata sporočila katera si medsebojno izmenjujeta.

Nasprotno pa asimetrični kriptosistemi ne uporabljajo enega ključa, pač pa dva: zasebni in javni ključ. Vprašali boste:

Zakaj rabimo dva ključa?

V asimetrični kriptografiji se en ključ uporablja za kodiranje podatkov, tj. javni ključ, drugi pa za dekodiranje kodiranega sporočila (e.g. chipertext), tj. zasebni ključ. Ko kodiramo sporočilo z uporabo Bobovega javnega ključa, to isto sporočilo lahko dekodiramo z uporabo Bobovega zasebnega ključa. Poleg tega, mora biti Bobov zasebni ključ, kot že ime pove, skrit tudi Bobu. To je edini ključ ki lahko dekodira katero koli sporočilo kodirano z Bobovim javnim ključem.

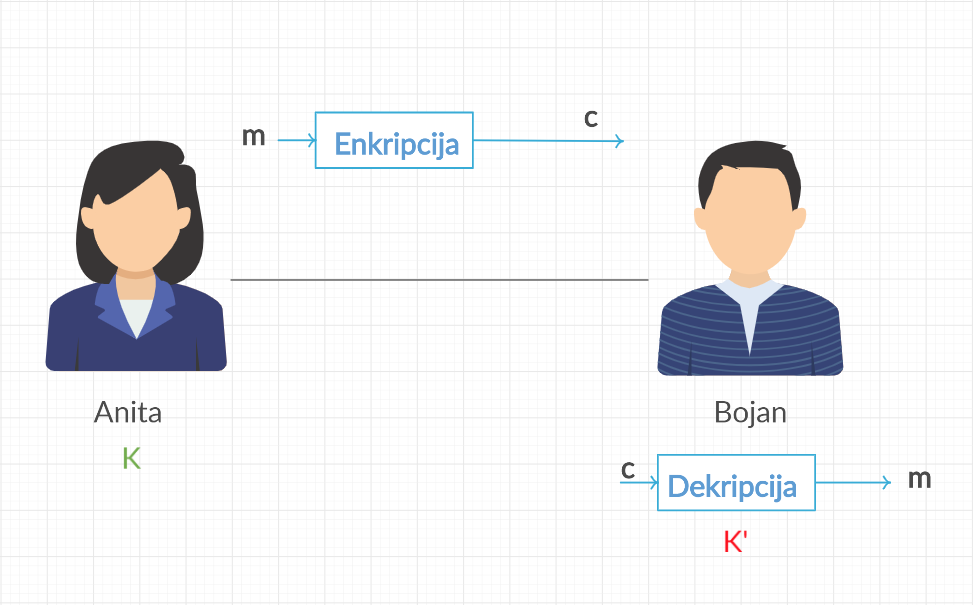
Javni ključi, kot nakazuje ime, so javni in varnost zanje ni zahtevana, ker bi morali biti javno dostopni in posredovani na svetovnem spletu. Javni ključ je uporabljen za šifriranje sporočila, ki je lahko odšifriran z uporabo zasebnega ekvivalenta. Za lažje razumevanje kaj se dogaja ko kodiramo z asimetričnim kriptosistemom, poglejmo zgornjo sliko.

Na zgornji sliki lahko vidimo da Alice uporablja ključ $K$ za kodiranje sporočila, katero Bob dekodira z drugačnim ključem $K'$. $K'$ je njegov zaseben ključ in $K$ je javni ekvivalent ključa $K'$. On a picture above, we can see that Alice uses key $K$ to encrypt the message, which then Bob decrypts with a different key, $K'$. $K'$ is his private key, and $K$ is $K'$’s public counterpart.

Na tej točki bi morali: 1. razumeti kaj so kriptosistemi 2. se zavedati razlike med simetrično in asimetrično kriptografijo (kodiranje) 3. poznati vsaj dva simetrična kriptosistema

Kaj pa asimetrični kriptosistemi? Poznamo kakšne? Seveda. Predstavimo jih nekaj.

7.5 Naš prvi asimetrični kriptosistem: RSA

RSA kriptosistem so iznašli Ron Rivest, Adi Shamir in Leonard Adleman leta 1978. V praksi je RSA počasnejši zato je redko uporabljen za kodiranje podatkov, bolj pogosto je uporabljen za kodiranje in podajanje simetričnih ključev, ki dejansko šifrirajo hitreje.

7.5.1 Kako deluje?

Za razlago kriptosistema RSA bomo uporabili manjše številke, ampak pomnite da realna vrednost večine $\mod(p)$ algoritmov ? ko uporabljamo primarne številke.

V prvem delu bomo pokazali kako delujejo kodirne in dekodirne funkcije ter pojasnili zakaj. Začnimo.

Dobili smo sporočilo (‘HELLO’) in izbrali dve dvojici, vsako z dvema številoma (izbiro bomo pojasnili v nadaljevanju). Očitno ni aritmetične operacije katero lahko prikažemo z nizom, zato mora biti sporočilo spremenjeno. Recimo da se ‘HELLO’ spremeni z uporabo konverzijskega algorithma v ‘2’. Ponavadi uporabljamo različne tehnike da združimo sporočilo in razdalje padding, z obliko ključev.

Fantastično, sedaj imamo vse kar rabimo. Pošljimo sporočilo skozi funkcije ki bodo v teoriji kodirale sporočilo:

Imamo torej osnove RSA algoritma in kako je oblikovana funkcija. So there we have the basics of the RSA algorithm , and how the trapped function is laid out.

Zanimivo je, kako smo prišli do teh številk, in kako je (5,14) povezano s (11,14). Začnimo.

7.5.2 Podrobnosti izbiranja para za dešifriranje / šifriranje

Sedaj predstavljamo korake v fazi vzpostavitve :)

Najprej izberemo dve praštevili. Na primer,
```
P = 2 and Q = 7
```
Drugič, pomnožite “P” in “Q”. Rezultati postanejo modul šifriranja RSA.
```
N = P * Q = 14
```
Tretjič, sestavite seznam med 1 in $ N $ in odstranite številke, ki imajo skupne faktorje z “N”:

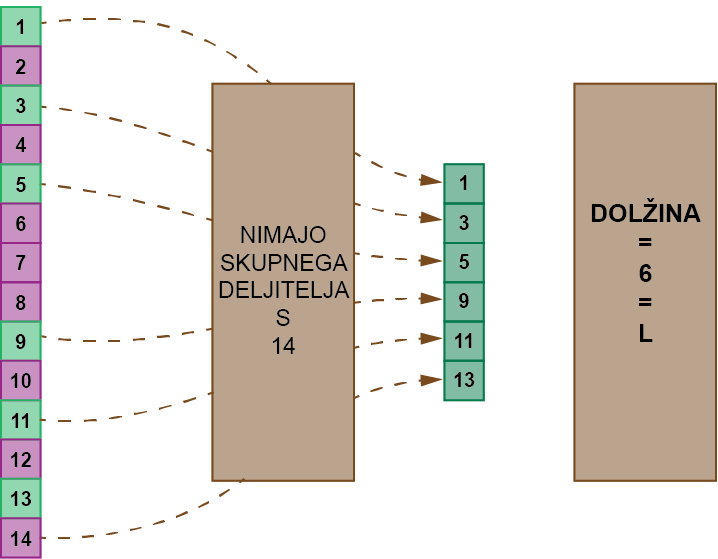
Izračunajte dolžino L = LengthNCF(14) na seznamu rezultatov. To lahko preprosto izračunate in sicer tako: ( Q - 1 ) * ( P - 1) = L
Izračunamo tako: L = (7 - 1 ) * ( 2 -1 ) = 6.

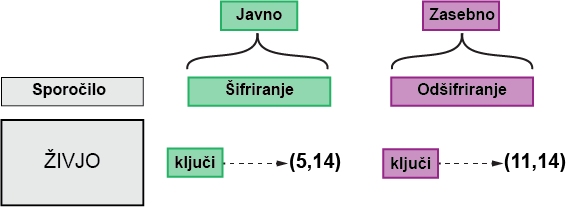
4. Zdaj je čas, da izberete šifrirni ključ. V primeru je bilo (5,14) in vemo, da je 14 modul.

Ko izberete šifrirni ključ, je nekaj pravil, ki jih ne smete spregledati: * Šifrirni ključ mora biti med 1 in L, t.j. od[2,3,4,5] * Šifrirni ključ mora biti primeren za “L” (6) in modul (14). V našem primeru obstaja samo ena možnost za šifriranje (javnega) ključa in to je 5. Tako smo prišli do zaključka, zakaj je javni ključ enak (5,14).

Nazadnje izberemo del za dešifriranje, zasebni ključ. V primeru je bil izbran $(11,14)$. 14 je modul, kaj pa 11?
Označimo ga z D.
To je zato, ker mora biti Decryptor (11) (zasebni ključ) pomnožen z modulom Encryptor (5) (publc) dolžino “L” enako 1!

D * E % LNCF(N) = 1
11 * 5 % 6 = 1

Če želite dobiti “D”, lahko naredimo seznam vseh številk od 1 do “T”, tj. “L” je enako 1.
Pri nastavitvi “T = 50” dobimo naslednje:

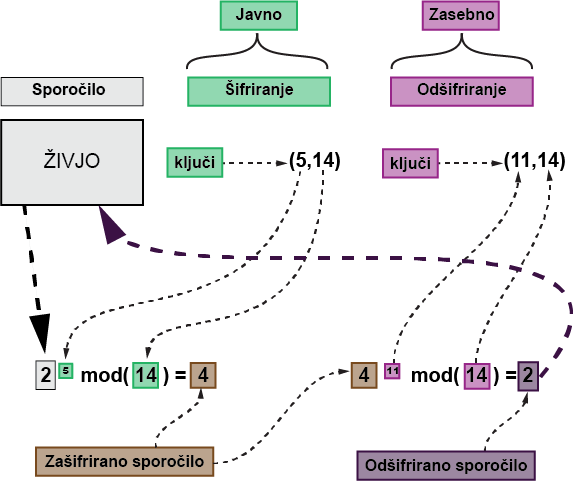
Poglejmo, ali lahko prejeta številka uspešno dešifrira sporočilo :). Zapomnite si, da je šifrirano sporočilo “4” in da je dešifrirano sporočilo “2”. Tako bi morali dobiti nekaj takega:

4 ** D % 14 = 2 <---Dešifrirano sporočilo

Naredimo torej majhen seznam razumevanja, da vidimo, ali pravilo deluje:

In je delovalo! Dobro opravljeno. Vidite, kako je uporaba funkcije za vse ključe za dešifriranje, ki sledijo pravilu (D * E% L = 1), uspešno dešifrirala sporočilo. Upamo, da to ni bilo preveč zapleteno :).

7.5.2.1 Opombe

Za šifriranje in dešifriranje sporočil moramo vedeti, kako izračunati moč števila v aritmetiki modula. Pokazali smo, kako je to storjeno v prejšnjem poglavju . Podali smo tudi aplikacijo, ki nam le-to pomaga izračunati .

V 4. koraku dejansko iščemo vse številke, ki so koprime z ‘L’. To lahko storimo z uporabo Eratostenovega rešeta iz prejšnjega poglavja .

V petem koraku dejansko iščemo inverze modula “N”, multiplikativno. Tako lahko uporabimo interakcijo iz prejšnjega poglavja .

V praksi je izbrana možnost “E” majhna, tako da je šifriranje hitro.

Opozorilo

Ne uporabljajte tega ali katerega koli drugega algoritma naivno!

7.5.3 Varnost RSA

Podrobna varnostna analiza je izven obsega branja, vendar pa je ključnega pomena omeniti obstoj več varnostnih lukenj, ki jih je treba upoštevati v instancah.

7.5.3.1 Možne varnostne luknje:

Potrebna je uporaba “varnih” praštevil “P” in “Q”. Zlasti „P-1“ in „Q-1“ bi morala imeti velika praštevila,
“P” in “Q” ne smeta imeti enakega števila,
$ E $ ne more biti premajhen,
Ne uporabljajte istega $ N $ za različne $ E $,
Vedno pad.

7.5.4 RSA v “resničnem svetu”

Šifriranje RSA je del mnogih standardov, to so: PKCS, ITU X.509 (ANSI X9.31, IEEE P1363) Poleg tega ga uporabljajo: SSL, PEM, PGP, Entrust itd. Standardi določajo številne podrobnosti o izvajanju, npr.:

$ E $ je treba izbrati kot majhno, vendar ne premajhno število,
‘multi praštevilo’ različice uporabljajo ‘N = PQR’ itd. Zaradi tega je ceneje dekodirati predvsem vzporedno z uporabo kitajskega izreka o ostankih .

7.6 Asimetrični kriptosistem na osnovi grafov

Spoznajmo še primer kriptosistema z javnimi ključi. Ta temelji na teoriji grafov, kar pomeni, da ga lahko enostavno prikažemo.

7.6.1 Uvod v teorijo grafov

Predstaljajmo si zemljevid s cestami in križišči. Vemo, da so križišča so med seboj povezana s cestami. Če se nahajamo na križišču lahko gremo po poljubni cesti do sosednjega križišča. Zemljevid je lep primer grafa. Imamo vozlišča (križišča), ki so med seboj povezana s povezavami (cestami). Dve vozlišči (križišči) sta sosednji, če obstaja povezava (cesta) med njima. Poglejmo si še pravo matematično definicijo

Graf je urejen par $G = (V, E)$, kjer je

$V$ neprazna končna množica vozlišč grafa $G$ in

$E$ množica povezav grafa $G$, pri čemer je vsaka povezava par točk.

Zdaj bi radi postavili sirene na križišča. Njihov zvok seže do vseh sosednjih križišč. Zanima nas, kam jih moramo postaviti, da pokrijemo vsa križišča. Odgovor imenujemo dominating set. To je množica vozlišč (križišč s sirenami), da je vsako drugo vozlišče (križišče brez siren) sosed vsaj enega od vozlišč v dominating setu (križišč s sirenami). Če zatevamo še, da moramo na vsakem križišču slišati natanko eno siren, da se njihov zvok ne meša, dobimo poseben primer dominating seta, ki mu rečemo exact dominating set. Tu mora biti vsako vozlišče, ki ni v exact dominating setu sosed z natanko enega vozlišča iz exact dominating seta. Sledi še formalna definicija

Naj bo $G = (V, E)$ graf. Dominating set je množica vozlišč $V_{DS} \subseteq V$, kjer za vsako vozlišče $v' \in V \setminus V_{DS}$ obstaja tako vozlišče $v \in V_{DS}$, da velja $\{v', v\} \in E$.

Če velja, da za vsako vozlišče iz $v' \in V \setminus V_{DS}$ obstaja natanko eno vozlišče $v \in V_{DS}$, da velja $\{v', v\} \in E$ in še, da nobeni dve vozlišči iz $V_{DS}$ nista sosednji, potem tak poseben primer dominating seta imenujemo exact dominating set.

7.6.2 Kako deluje?

Ker je to asimetričen kriptosistem, pomeni, da imamo javni in zasebni ključ. Javni ključ je celoten graf, zasebni pa exact dominating set tega grafa. V dovolj velikih grafih je zelo težko najti exact dominating set, kar pomeni, da iz javnega ključa ne moremo izračunati zasebnega.

Kriptosistem deluje le za šifriranje števil. Če želimo zašifrirati besedilo, ga moramo najprej spremeniti v število. V interaktivnem delu za abecedo uporabljamo male črke angleške abecede in šumnike, kar skupaj nanese 29 znakov. Torej, sporočilo predstavlja število v devetindvajsetiškem sistemu, ki ga moramo le pretvoriti v desetiškega, da bomo z njim lažje računali. (V interaktivnem delu pretvarjamo sporočilo v število malo drugače, da dobimo lepše rezultate.)

Bojan želi poslati sporočilo Aniti, zato ga mora pretvoriti in dobi število $M$. Nato ga zašifrira z Anitinim javnim ključem po naslednjih korakih. Za enostavnejši zapis naj bo $n$ število vozlišč v grafu (Anitinem javnem ključu).

Sporočilo $M$ zapiše kot vsoto $\sum_{i=1}^n w_i$, kjer so $w_i$ naključno izbrana števila (razen zadnjega).
Vsakemu vozlišču $v_i \in V$ priredi člen vsote $w_i$: $\text{čistopis}(v_i) = w_i$.
Za vsak $v \in V$ naj bo $\text{sosed}(v) = \{v' |\{v, v'\} \in E\} \cup \{v\}$ množica vseh sosednjih vozlišč vozlišča $v$ skupaj z $v$. Definiramo funkcijo $\text{kriptogram}(v) = \sum_{v' \in \text{sosed}(v)} \text{čistopis}(v')$, ki vsakemu vozliscu priredi vsoto vseh njegovih sosedov (vključno z vozliščem samim). Definirana funkcija predstavlja zašifrirano sporočilo.

Ko Anita prejme kriptogram, uporabi svoj zasebni ključ (exact dominating set), da odšifrira kriptogram tako, da sešteje vrednosti na vozliščih, ki so del exact dominating seta. Razmisli, zakaj to drži?

Zdaj, ko poznamo šifriranje in odšifriranje, si moramo pogledati še kako zgeneriramo javni in zasebni ključ. Ker je težko najti exact dominating set v grafu, bomo začeli tako, da narišemo vozlišča, ki bodo tvorila exact dominating set. To pomeni, da ta vozlišča ne smejo biti povezana med seboj, in da morajo biti vsa ostala vozlišča povezana z natanko enim izmed njih. Potem dodamo poljubno število ostalih vozlišč in vsakega takoj povežemo z enim iz exact dominating seta. Ker je zaenkrat očitno katera vozlišča tvorijo exact dominating set, moramo dodati še naključne povezave med ostalimi vozlišči. Tako smo sestavili graf za katerega poznamo njegov exact dominating set.

Zdaj, ko si vse predstavljamo, pa se vrnimo k vprašanju, zakaj odšifriranje deluje. Torej trdimo, da velja \[ \sum_{v \in V_{EDS}} \text{kriptogram}(v) = \sum_{v \in V} \text{čistopis}(v) = M, \] kjer je $V_{EDS}$ exact dominating set.

To sledi iz definicije exact dominating seta, ki pravi, da je vsako vozlišče sosednje natanko enemu vozlišču iz exact dominating seta ali pa je del njega.

7.6.3 Varnost

Spoznali smo primer asimetričnega kriptosistema, ki si ga brez težav predstavljamo. Prav tako že vemo, da če je graf (javni ključ) dovolj velik, ne moremo izračunati njegovega exact dominating seta (zasebni ključ).

Lahko pa izračunamo sporočilo iz kriptograma brez zasebnega ključa tako, da rešimo sistem linearnih enačb. Sistem linearnih enačb dobimo, če za vsak $v \in V$ zapišemo enačbo: \[ \sum_{v' \in \text{sosed}(v)} \text{čistopis}(v') = \text{kriptogram}(v). \] Iz tega sledi, da ta kriptosistem ni varen.