Poglavje 1 Keys

Ciphers and more generally cryptosystems are controlled by keys. which determine how data is modified. Of course the keys can have a digital form. When we will compare their size, we will assume they are in the form of a binary sequence:

01001101010101… We follow Kerckhoffs’ principle which assumes:

the “adversary” knows the cryptosystem and all the algorithms used, but does not know the keys, which provide security.

Slika 1.1: In a cryptographic jargon we say that we try to break the cryptosystem.

Before we dive deeper into cryptography, let us think about everydays life. The keys that are the most common in the digital world are passwords and PIN (Personal Identification Number). For the first one we are suppose to use as reach list of characters, while in the second case we use only digits 0..9 (since usually a keyboard has no other characters).
In old times (even BC) city fortifications had guards guarding the city gates. They were armed with weapons and in turbulent times they did not let in anyone who did not know the correct password.

Slika 1.2: What happened to those who said the wrong password? The rule was, Take care of them!

1.1 Passwords and attacks on them

Passwords allow us to control access to most computers (including phones today). There is almost no person in the modern world who does not use passwords every day and practically everywhere, e.g. to log in to email, social media accounts, to our workspace, to access stored data, money, etc. The problem of the spy dilemma, however, remains essentially unchanged.

How do we know if we can trust
someone who wants a password from us?
Maybe someone is listening to us or recording us.

How to prevent such attacks?
Someone has patented a graphical keyboard that randomly shuffles the numbers on the input keys, while allowing the numbers to be read only at a certain angle.

Slika 1.3: The spy’s dilemma. In a dark night a spy was returning to the castle after a diversion in the enemy’s camp. Near the wall, he heard a voice from the darkness.
How does a spy convince a guard that he knows the password without betraying it to a potential intruder or eavesdropper hiding nearby?

Good password
1. is easy to remember
2. it is hard to guess.
These two criteria, of course, often contradict each other.

Slika 1.4: A password is like a toothbrush.

If the password is hard to remember, then people usually write it down or they forget it and have to regain access in a special and vulnerable way. When setting a password on a computer, we can encounter many restrictions, such as it should:
1. have at least 8 characters,
2. contain at least one letter and
3. contain at least one number, etc.

The reasons for this are obvious from Table 1.

Example	# characters	Complexity	Password length	Time to break it
kitty	5	25 (small letters)	24 bits	less than 2 seconds
br1a9Az	7	62 (leters and digits)	42 bits	5 days
TH,X1lbV+	10	95 (keyboard chars)	66 bits	233977 years

Table 1. Guessing passwords, taking into account that our computer
(e.g. our smartphone) checks 10 million passwords per second.

An attacker may also have more computing power available than our phone or computer, so we have to think about the options (see Tables 2 and 3).

Attacker	Decryption speed
an individual, 1 PC	(\(2^{17}\) - \(2^{24}\) keys/sec)
a small group, 16 PC	(\(2^{21}\) - \(2^{28}\) keys/sec)
an academic network, 256 PC	(\(2^{25}\) - \(2^{32}\) keys/sec)
big company with 1.000.000 USD for hardware	(\(2^{43}\) keys/sec),
Military inteligence services with $1.000.000.000 for hardware and advanced technology	(\(2^{55}\) keys/sek).

Tabela 2. Brute force attacks - how many keys can we check in one second.

Key length (in bits)	Individual attacker	Small groups	Research networks	Large companies	Military intelligence services
40	days	hours	minutes	miliseconds	mikroseconds
56	centuries	decades	years	hours	seconds
64	millenia	centuries	decades	days	minutes
80	\(\infty\)	\(\infty\)	\(\infty\)	100 millenias	centuries
128	\(\infty\)	\(\infty\)	\(\infty\)	\(\infty\)	\(\infty\)

Table 3. Brute force attacks - how much time do we need for different key lengths.

One possible defense is that after three incorrect password entries, the system freezes, for example for 20 seconds.

1.2 Password statistics

The above mentioned system requirements were quite common, but we will realize that they did not significantly contribute to security (especially if the user has a password really written on a piece of paper and forgot it next to the computer). Let us see anyway what happens when there are no such restrictions (there is almost 80% of such
in the case of cloud services, see e.g. [McAfee] (https://www.vpncrew.com/passwords-facts-and-statistics/)). It often happens that that some larger database of passwords has been compromised. This gives us insight into human habits.
At Linkin over 80% of user passwords had length 6-10 characters, of which more than 30% had length 8. Password statistics at [Rockyou] (www.rockyou.com), where 32 million unsecured passwords were examined, the most common password is 123456 (0.11%). It is followed by 12345 (0.04%), 123456789 (0.04%) and then 1234567 (0.02%), 12345678 (0.02%).
They were in the top ten more password (0.03%), iloveyou (0.03%), princess (0.02%), rockyou (0.02%), abc123 (0.02%). 40% of passwords contained only lowercase letters, 15% only numbers, 35% only lowercase letters and numbers, while only 4% also contained them special characters. The use of variations on the theme of simple passwords is also known, e.g. various combinations of the word “password”, the number 123 and the trinity “abc”. They are also common names of months and days of the week. At the end of the password we find punctuation - e.g. dots, numbers or even years.

The password to launch a nuclear missile has been “0000000” for 20 years.
The Facebook used “Chuck Norris” as the main password to access all profiles.

To make matters even worse, almost 30% of users use the same passwords on many devices and accounts. The latter is not surprising, since 70% of users have at least 10 accounts protects only with passwords. This number will only grow, so applications are being used to manage passwords. However, if you use yours for this purpose popular browsers, you must also have a master password set. master password). However, if we talk about similar passwords on different devices, the share increases to 50%. 66% of people use 1 or 2 passwords for all their own accounts: The person usually changes the password every 2.5-3 years.

1.3 How do we remember more secure passwords?

Passwords that contain more than one meaningful word are called passphrase. This phrase do not have to mean anything, words can be taken out of context.

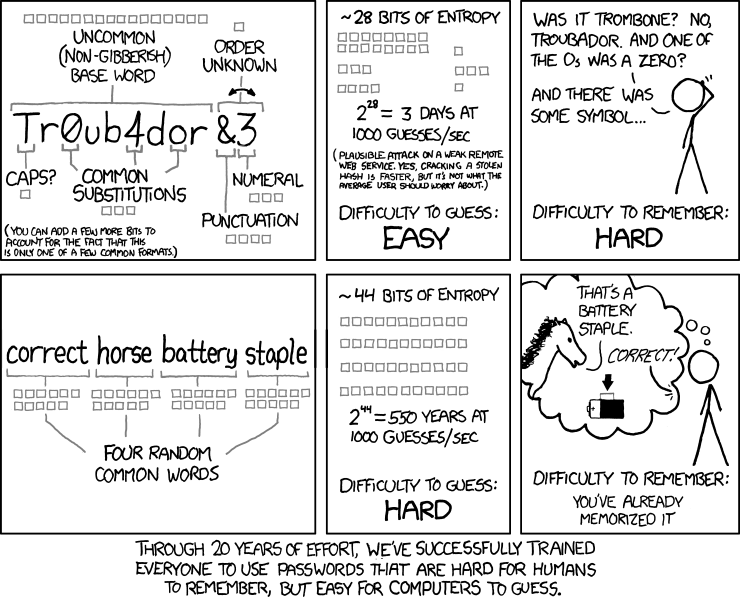
Slika 1.5: For over 20 years, we have been trying to train users to use passwords that people have a hard time remembering, but computers can still guess them quickly.

1.4 Introducing and authorizing

To put it simply, identification is the disclosure of a user’s identity, authentication is a procedure (for us it will often be a cryptographic protocol), where the user wants to confirm that he is really who he claims to be.

*Alice and Bob share the secret key K, which they use for encryption

1. Bob selects a 64-bit X challenge and sends it to Alice.
   
2. Alice calculates Y = K XOR X and sends it to Bob.
   
3. Bob calculates Y’= K XOR X and checks if Y = Y’.*

Identification protocol “challenge and response”. One could replace the operation XOR by some other function, e.g., \(y=e_k(x)\) and \(y'=e_k(x)\) and still check \(y=y'\). Almost all schemes use challenge and response protocols, however, the most useful do not use shared keys (because they exceed our current level, let us leave them for another time).

A case study (health card and terminal authenticate each other):

Slika 1.6: An example of an application that uses the challenge and response protocol. How does Slovenia’s health card and a terminal authenticate each other? First, both the terminal and the card must be able to generate random numbers. What about the keys? The terminals have a master key \(M\) and a group key \(K_S\), but they do not have the space to store the keys of all users. Therefore, each user \(U\) with serial number SN is assigned a key \(K_U: = e_M\)(SN) using the master key and its serial number SN, and all group keys to identify different groups (except the group of terminals are here also medical cards, cards of various pharmacies, etc.

A subset of the following three properties is used to verify the user’s identity:

1. something that the user knows - e.g. passwords, numbers (PIN),
   
2. something that the user is - these are biometric data based on the physical characteristics of the user, such as fingerprint, iris, face, gait.
   
3. something that the user has - i.e., security tokens such as physical keys, identity card, driving license, bank card, etc.
   
   

   Slika 1.7: Biometric tests. It should be noted that there is no ideal test. Fingerprints e.g. we leave on various objects we touch. If we are in water or cold for a long time, the fingerprint changes a bit. The problem also arises if we injure our finger. Can you imagine having to take a bite at an ATM? Does anyone remember the actual verification of the signature, it should be done only by a trained graphologist.

In the case of a payment by a bank card, usually two properties are used: bank card (something the user has) and PIN (something the user knows).

1.5 Key management

Let us ask some basic questions:
1. Where do we get the keys from?
2. Why do we trust keys?
3. How do we know whose key we have?
4. How to limit the use of keys? 5. What happens if a private or secret key is compromised (lost)?
6. Who is responsible?
7. How to recall a key?
8. How do we enable nonrepudiation service?

These issues apply to both symmetric (secret) as well as public and private keys.

The main goal is to maintain the privacy and integrity of the keys, which must be guaranteed at all times. For each key, this means from the time a key was generated and until the key is no longer in use and has been destroyed, see Fig. 8.
In fact, almost allways the key has been replaced with a new key, which means this is a cyclic process in which the key-destruction is followed by an installation or inclusion of a new key. However, this new key is generated, distributed and stored before the old one was destroyed. In some systems, we still have an extra request that the keys be archived.

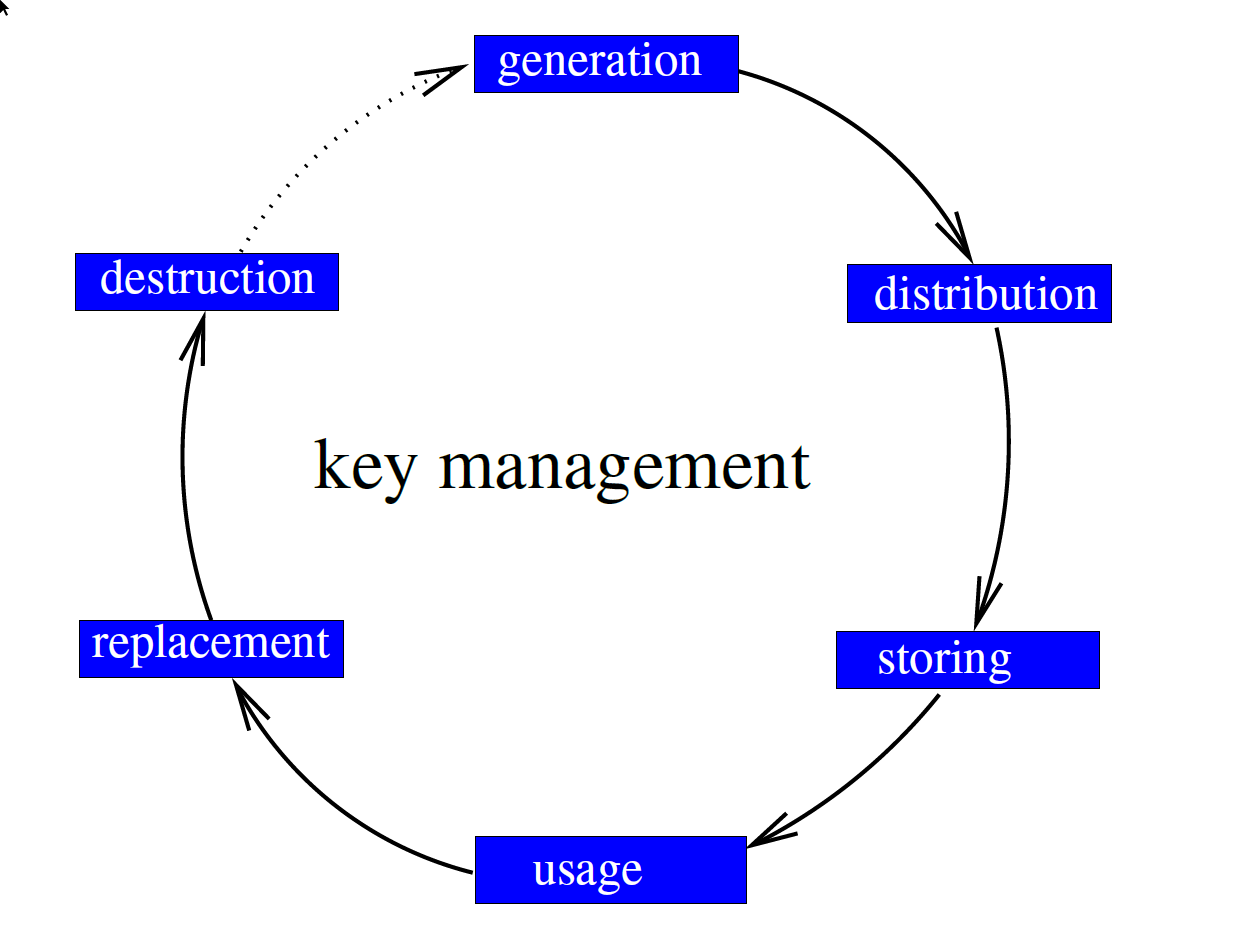
Slika 1.8: The main life cycle stages are shown in the following diagram.

Control levers are required throughout the life of the key. That ranges from audit trails to logs the use of keys, which of course do not make sense without supervision and authorization of an appropriate response/action in case the key has been compromised. Therefore, it is often (especially in larger systems) desirable that the keys have the appropriate owners who are responsible for their protection.
In the case of algorithms for symmetric cryptosystems, one can use an arbitrarily sequence of bits (occasionally also other characters), which means that most can users itself generates their keys. They must be unpredictable: often we use
- manual methods, e.g. tosing a coin or dice,
- derivation from personal data, e.g. PIN or
- (pseudo) random number generators (RNG).

Asymmetric systems: generating large primes requires “sophisticated” mathematical processing and may require considerable power/space/time. Users are sometimes forced to trust outside generated keys or software. To illustrate: in the case of the RSA cryptosystem, its security is reduced to the attacker’s ability to factorize the module n. If the process of generating keys gave only a limited number of prime numbers, the attacker could generate the same primes and then check for each of them if it divides n.
Distribution of keys and safe storage are central of importance. The problems we encounter and their solutions are mostly similar, therefore, we consider them together. Reason to use strong cryptographic systems is to prevent an attacker from calculating the key. Of course, all this does not make sense, if an attacker can find them unprotected somewhere on the system.

Correct 5 bad habits that affect the security of passwords or. more general keys
1. Do not choose common (generic) passwords or keys of a special form.
2. Do not store passwords or keys in less secure (too obvious/omitted) places.
3. Do not use the same passwords and keys in different programs (do not recycle passwords or keys)
4. Do not send or share passwords and keys (toothbrush) with anyone.
5. Do not copy passwords and keys (copy/paste via clipboard).

5 good practices for password security or. more general keys
1. Passwords and keys should be long enough.
2. Update/restore/change your passwords and keys frequently (and do so as soon as you know your account has been compromised).
3. Secret phrases are a good strategy for remembering passwords (at least the main ones).
4. Use multi-level (factor/factor) authentication for important/critical accounts (if possible).
5. Use a good key and password management program.

Problems

1. How much is GREAT (and computational power)? We only live 2-3 billion seconds. For kilo K (\(10^3\)), mega M (\(10^6\)), giga G (\(10^9\)), and tera T (\(10^{12}\)), which we have just got used to, are followed by units of the heel P (\(10^{15}\)), exa E (\(10^{18}\)), son-in-law Z (\(10^{21}\)), in jota Y (\(10^{24}\)). The latter is in the range of the number \(2^{80}\) (why?), Which is the size of the space from which you like in cryptography public keys, we randomly select a secure key (perhaps precisely because we don’t use it much today).

• How many different characters are on your keyboard (don’t forget the lowercase and uppercase letters)? Would you be able to list them all?
• How many grains of rice are on average in one kilogram of rice (surely you have some at home)? Why is the word average in the question? Does that mean you’ll have to count multiple times?
• How many possible passwords would there be if you chose a word in the Slovenian language as your password? What if you chose two or three words? What if we didn’t limit ourselves to Slovene? How many different languages ​​are there in this world?
• How much exa rice did the king promise (from the story of the king, chess and rice)?
• let’s say we ask ourselves about the number of our ancestors and calculate that they had children on average at the age of 25, then 2,000 years ago they could have had a maximum of \(2^{80}\) (why?), which, of course, is not possible (why?). But how many ancestors would an average person discover if they had the opportunity to research 2K years ago?
  

2. Accounting capacity for breaking passwords: (a) yours, (b) your surroundings, (c) if you had more resources available \(\dots\)
3. Do you have a plan B in case you forget your password/key? Eg. passwords stored in a notebook that only you know where they are stored.
4. How many different accounts and passwords do you use (or estimate that you will use them in the next 10 years)?
5. List the good and bad features of password recovery via email. Good: quick fix if you forget your previous password. The bad: if someone hacks into your email, they can access the link for password recovery and change it.
6. Suggest some solution to the spy dilemma (see Fig. 3). Enter an additional password, e.g. soldiers should agree that in addition to the password possibly greet with a special word, then say the password.
7. How exactly does password verification work? Can we avoid storing passwords somewhere (because, as we mentioned, such a database can get out of control, even if we try so hard)? Some companies have password lists for their employees. Where should they be kept? This can be avoided by not having too many accounts and using passwords that you can easily use Remember and are logical for us, but not for others.
8. Suggest some function \(e_k(x)\) (see Challenge and Response Identification Protocol) and consider what its good and bad properties are.
9. Find any answers to the basic key management questions we asked at the beginning of Section 5.
10. List the good and bad properties of individual biometric tests. The advantage of all of them is that they are unique in each individual. The downside of a fingerprint is that it can happen to anyone changes to the individual, taking a tooth bite is an extremely unhygienic procedure, the voice may be distorted during the examination or but a recording of our voice is used.
11. How would you derive a key from personal data so that an attacker could not help himself (remember the Kerchoffs principle). To compile the keys, we would use personal data that the attacker certainly cannot access, e.g. hour of birth.
12. List the good and bad properties of the above good habits for choosing passwords/keys (Tables 3 and 4). Could you supplement both lists with three more recommendations?
    
13. Find some good password cracking program and study how it works.
14. Who would I contact if I had to implement secure password checking in my application? How to avoid this?
15. Estimate the computational power required to break a secret phrase in one year.