Poglavje 3 Kratice
3 Uvod
Krajšanje oz. zgoščevanje (ang. hash) je postopek, pri katerem poljubnemu nizu znakov dodelimo neko (kratko) oznako, ki ji bomo rekli kratica oz. zgostitev (tudi izvleček ali digitalni prstni odtis). Npr. do tega pride običajno v šoli, ko učence na začetku šolskega leta razporedimo v razrede, npr. 150 učencev v 4 razrede A-D (37+38+37+38). Sedaj je enostavno poklicati četrtino učencev (A-jevci pridite na štart!). Recimo, da imamo v skupini 5 učencev: Janez Korenina, Zala Novak, Miha Copatar, Zvonko Nagode in Tone Rastlina. Vzamimo, da tokrat postopek krajšanja za vhod prejme učenca in ga zapiše kot niz začetnic njegovega imena in priimka. Dobimo torej vrednosti, kot so JK, ZN, itd.
Oglejmo si še en primer. Zjutraj greš z družino na zajtrk. Vsak član družine naroči natakarju, kaj bo jedel in pil, na koncu pa pridni natakar, ki hoče biti prepričan, da se ni zmotil pri zapisovanju naročila, vpraša: “Torej skupaj boste 2 kavi in 3 rogljičke, je tako?” Pravkar opisan postopek, ki ga je uporabil natakar, je res zelo primitiven primer zgoščevanja. Kaj je v bistvu naredil? Vzel je dolgo sporočilo, kjer je vsak član družine naročil nekaj zase, in ga predelal v krajšega, ki služi temu, da preveri, ali je med prenosom informacije prišlo do napake.

Slika 3.1: Začetnice učencev
Naštejmo nekaj primerov, kjer se krajšanje oz. zgoščevanje uporablja:
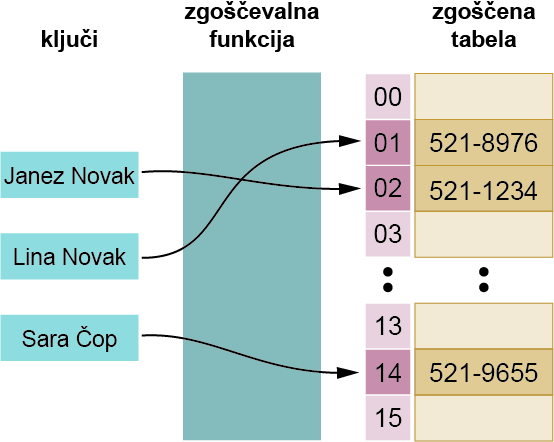
Shranjevanje podatkov v tabeli. Namesto, da iščemo nek zapis po tabeli, lahko izračunamo zgostitev in takoj skočimo na mesto v tabeli, na katerega se sklicuje ta zgostitev. Tukaj je pomembno, da pri zgoščevanju prihaja do čim manj sovpadanj, ki jih v kriptografiji imenujemo trčenja (ang. collision).
Preverjanje enakosti podatkov. Tu želimo, da tudi najmanjša sprememba v vhodnem nizu vrne čim bolj različno zgoščeno vrednost. Krajšanje se uporablja predvsem pri preverjanju pravilnosti oz. enakosti podatkov. Če imamo na voljo zaupanja vredno zgostitev nekih pomembnih pridobljenih podatkov, ki bi jim radi zaupali, lahko zgostitev izračunamo še sami in zgostitvi primerjamo. Če sta enaki, so podatki najverjetneje identični. S tem pristopom se lahko zelo pohitri obdelavo podatkov. Uporablja se npr. pri prenosu večjih datotek.
Hranjenje gesel. Namesto, da bi hranili gesla v svoji prvotni obliki, shranimo v bazo namesto tega zgoščene vrednosti gesel. Tako zagotovimo, da gesla uporabnikov ostanejo neznana, tudi če napadalec vdre v naš sistem. Magnetni trak na bančni kartici npr. vsebuje zgostitev našega PINa. Vendar se tu zgodba ne konča. Zaradi takšnega shranjevanje gesel so nastale t.i. mavrične tabele, ki vsebujejo slovar gesel, ki so jih nepridipravi odkrili do sedaj v različnih aplikacijah, in njihovih zgoščenih vrednosti. To pa lahko rešimo na enostaven način, in sicer tako, da uporabnikovemu geslu dodamo t.i. sol. To je naključen niz, ki ga potem skupaj z geslom zgostimo in shranimo v podatkovno bazo. Ta naključnost zagotovi, da v mavričnih tabelah, tudi če obstaja zapis za geslo, ne najdemo takšnega zapisa.
3.1 Primeri
Zgoščevalne funkcije so vsepovsod okoli nas, poglejmo si nekaj primerov:
3.1.1 ISBN
ISBN (International Standard Book Number) je desetmestna (ali trinajstmestna) številka, ki enolično definira neko knjigo. Vsaka knjiga, tiskana po letu 1970, ima svojo ISBN številko. Prvih 9 oz. 12 števk označuje naslov knjige, avtorja, založbo in jezik, v katerem je napisana, zadnja cifra pa je zgoščena vrednost vodilnih cifer. Da bi izračunali to zgoščeno vrednost, vsako števko pomnožimo z ustreznim faktorjem, vsoto pa delimo s številom 11.
Natančen postopek samega izračuna lahko preveriš tukaj, sam pa lahko vzameš knjigo, ki ti je najbolj blizu, in poskusiš, če ta postopek deluje ali ne!
3.1.2 EMŠO
Na hrbtni strani našega osebnega dokumenta je zapisana številka EMŠO (enotna matična številka občana). Njena sestava je precej preprosta: datum rojstva določa prvih sedem števk, osma in deveta števka je pri nas vedno 50 (kar označuje rojstvo v Sloveniji), sledijo še tri števke, ki določajo zaporedno številko rojstva (pri tem se razlikuje med rojstvi otrok moškega in ženskega spola). Sledi še zadnja cifra, ki je v bistvu zgoščena vrednost vseh ostalih. Tukaj lahko poskusiš generirati svojo EMŠO številko, pa tudi tisto izmišljenih oseb. Poskusi odgovoriti na naslednja vprašanja:
Kako se spremeni EMŠO, če spremeniš ime?
Ali lahko imata dva občana isto EMŠO številko?
Kaj lahko sklepaš o imetniku dane EMŠO številke, če o njem veš samo EMŠO?
3.1.2.1 Izračun EMŠO številke:
3.1.2.2 Preverjanje EMŠO številke:
3.1.3 Številke plačilnih kartic
Tudi zadnja števka naših plačilnih kartic je zgoščena funkcija prvih petnajstih. Izračunamo jo s tako imenovanim Luthovim algoritmom, ki ima podoben postopek kot zgornja dva primera: ustrezno pomnožimo števke kartice, jih seštejemo, na koncu pa izvedemo še neko celoštevilsko deljenje. Na spletu najdemo več takih aplikacij, ki ponaredijo izmišljene kartice (v bistvu izberejo skoraj naključno prvih 15 cifer in izračunajo na koncu še kontrolno vsoto).Postopek, s katerim bi lahko trivialno preverili, ali so take kartice resnične ali ne, ne obstaja; to pa omogoča razna protizakonita obnašanja (na primer lahko vsak mesec generiramo izmišljeno kartico in tako koristimo “brezplačni mesec” na raznih spletnih straneh kot Netflix. Ponovimo pa, da je tako obnašanje protizakonito). Nekatere spletne strani odvzamejo iz računa 1 cent in ga takoj vrnejo z namenom preverjanja pristnosti kartice. Proti takemu sistemu za preverjanje kartic seveda spodnji postopek ni odporen.
Tudi s spodnjim pripomočkom lahko generiramo izmišljene kartice: vnesi prvih 15 števk, dobil pa boš veljavno številko kartice!
Zaključek
Iz zgoraj navedenih primerov bi moralo biti jasno, da osnovni podatki enolično določajo zgoščeno vrednost, obratno pa ne velja. Na primer, če se navežemo na zgornji primer ISBN-ja: obstaja namreč več milijonov knjig, vsaka ima enolično določeno ISBN kodo, z druge strani pa obstaja samo 11 zgoščenih vrednosti za podane osnovne podatke.
Podoben razmislek lahko uporabimo v računalništvu, tudi ko nas vsebina in nasploh pomen podatkov, ki jih prenašamo, sploh ne zanima. Na primer, da želimo sporočilo dolgo 20 bitov zgostiti v vrednost dolgo 5 bitov. V takem primeru imamo možnih 1048576 (\(2^{20}\)) vhodnih vrednosti, ki jih bo zgoščevalna funkcija razdelila v skupine, ki bodo imele isto zgoščeno vrednost; v povprečju bodo te skupine velike 32768 (\(2^{15}\)), osnovna želja je seveda, da so skupine čim bolj enakomerne. Trčenjem se seveda želimo izogniti.
3.2 Lastnosti
Zgoščevanje pa je eden izmed temeljnih gradnikov tudi v kriptografiji. Kriptografska zgoščevalna funkcija vzame nek vhodni niz in učinkovito (beri hitro) generira drugačen niz, zanjo pa si želimo naslednje lastnosti:
ponovljivost - funkcija ni odvisna od naključja, za določen vhod vedno vrne enak izhod (strokovnjaki pravijo, da gre za deterministično funkcijo),
krajšanje - vhodni niz poljubne dolžine pretvori v niz točno določene dolžine,
razpršena podobnost - majhna sprememba v sporočilu povzroči dobro zaznavno spremembo v zgostitvi (tj. stara in nova zgostitev ne izgledata podobno. V praksi si želimo, da bi sprememba enega samega bita na vhodu spremenila približno polovico izhoda.)
enakomernost - torej za dva različna vhoda ne dobimo enakega izhoda (to je v praksi zelo težko doseči in so ponavadi zadovoljive zgoščevalne funkcije, kjer je verjetnost sovpadanja dovolj majhna),
enosmernost - iz izhoda v doglednem času ne moremo izračunati vhoda.
Bi lahko rekli zgoraj vpeljani funkciji na učencih, ki smo jih priredili začetnice imen in priimkov, zgoščevalna funkcija? Pravilo 1 je izpolnjeno, saj bo Janez Korenina vsakič zgoščen v JK. Pravilo 4 ni izpolnjeno, saj Zala Novak in Zvonko Nagode tvorita enak izhod, tj. ZN. Verjetnost, da imata izmed petih učencev dva enake začetnice, je sicer majhna (1.6%), a v svetu zgoščevalnih funkcij je to ogromno. Kot primer lahko vzamemo tudi scenarij, kjer je v razredu 20 učencev. Takrat je verjetnost, da imata dva učenca enak izhod že 26.5% (paradoks rojstnih dnevov). Pravilo 2 je izpolnjeno, saj je izhod vedno dolžine 2 (ignorirajmo za zdaj primere, ko ima učenec več kot eno ime ali priimek, ali pa privzemimo, da smo vzeli samo prvo ime in prvi priimek). Pravilo 5 ni izpolnjeno, saj iz izhoda lahko vidimo, kakšen je bil vhod. Npr. ZN ne more biti nič drugega kot Zala Novak, saj je edina z začetnicami Z in N. Tudi v primeru, ko obstajata dva ali več učencev z istimi začetnicami, lahko omejimo možen nabor imen, ki jim pripada.
3.2.1 Razvoj kriptografskih zgoščevalnih funkcij
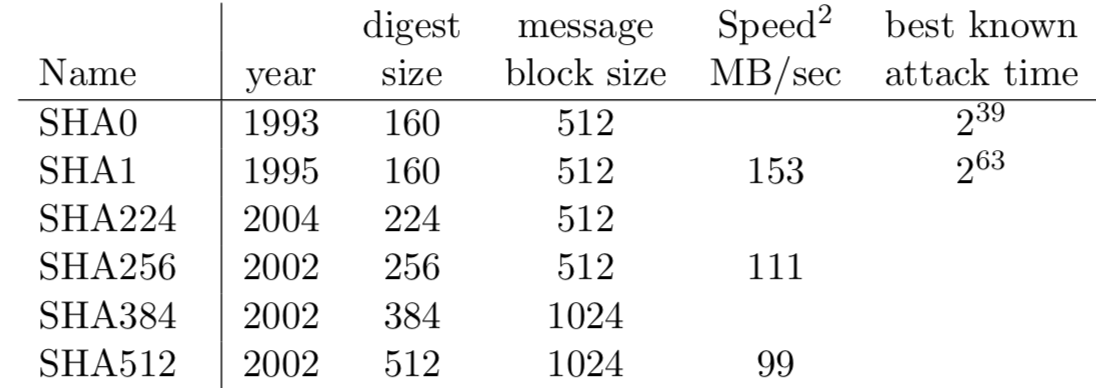
Kot smo videli, funkcija z začetnicami ni za resno uporabo, zato si moramo izmisliti boljšo zgoščevalno funkcijo. Na srečo pa lahko izberemo že kakšno izmed obstoječih, kot so SHA-256, SHA-512, Bcrypt in mnoge druge. Leta 1993 je Nacionalni inštitut za standarde in tehnologijo (NIST) objavil zgoščevalno funkcijo SHA-0 zasnovano na algoritmih MD4 in MD5. Kmalu jo je zamenjala njena izboljšana različica SHA-1, ki jo je predlagala Nacionalna varnostna agencija (NSA) (dodali so zamik za 1 na vsakem krogu). Dolžina vhodnega sporočila pri SHA-1 je omejena na \(2^{64}\) bitov in kot rezultat vrne zgostitev dolžine 160 bitov. Leta 2005 je bil na zgoščevalno funkcijo SHA-1 odkrit napad, s katerim je možno v manj kot \(2^{63}\) korakih poiskati različni vhodni sporočili z enako vrednostjo zgostitve. Zato je NIST leta 2008 objavil nov standard za zgoščevalne funkcije FIPS 180-3 [26]. Ta definira algoritme zasnovane na SHA algoritmu, ki vračajo zgostitve velikosti od 224 do 512 bitov in jih imenujemo algoritmi SHA-2, glej Pfleeger et al. [15, Sect. 12.4].
3.2.1 Paradoks rojstnih dnevov
To seveda ni paradoks, a vseeno ponavadi zavede naš občutek. Poglejmo si konkreten primer.
Na nogometni tekmi sta na igrišču dve enajsterici in sodnik, skupaj 23 oseb.
Kakšna je verjetnost, da imata dve osebi isti rojstni dan?
Ali je ta verjetnost lahko večja od \(0.5\)?
Čeprav je 23 relativno majhno število (glede na število dni v letu), je med 23 osebami 253 različnih parov. To število je veliko bolj povezano z iskano verjetnostjo. Testirajte iskanje parov s skupnimi rojstnimi dnevi na zabavah z več kot 23 osebami.
Slika 3.2: Nogometna tekma. Kakšno naključje! Mar res?
Organizirajte stave in dolgoročno boste gotovo na boljšem, na velikih zabavah pa boste zlahka zmagovali. Empirični (izkustveni) zaključek je naslednji:
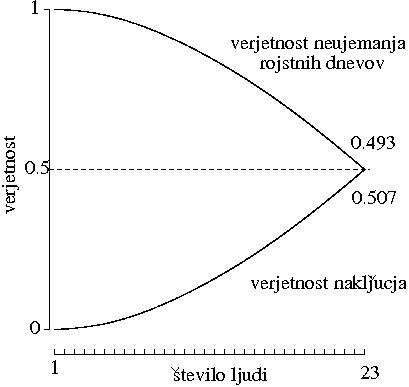
V poljubni skupini 23-ih ljudi je verjetnost, da imata vsaj dva skupni rojstni dan \(> 1/2\).
V nemškem nogometnem prvenstvu so preverili zgornjo trditev empirično tako, da so pregledali vse tekle v določenem letu. Sedaj pa jo uteljimo še z neposrednim računanjem verjetnosti. Ko vstopi v sobo \(k\)-ta oseba, je verjetnost, da je vseh \(k\) rojstnih dnevov različnih enaka:
\[ {365 \over 365} \times {364 \over 365} \times {363 \over 365} \times \cdots \times {365-k+1 \over 365} = \left\{ \begin{array}{ll} 0.493,\ & \mbox{če je $k\!=\!22$} \\ 0.507,\ & \mbox{če je $k\!=\!23$} \end{array} \right. \]
Slika 3.3: Graf za verjetnost trčenja
Ocenimo še splošno verjetnost. Mečemo \(k\) žogic v \(n\) posod in gledamo, ali sta v kakšni posodi vsaj dve žogici. Poiščimo spodnjo mejo za verjetnost zgoraj opisanega dogodka.
Privzeli bomo, da je \(|h^{-1}(x)|\approx m/n\), kjer je \(n=|Z|\) in \(m=|X|\) (v primeru, da velikosti praslik niso enake se verjetnost le še poveča). \[
\biggl(1-{1 \over n}\biggr)
\biggl(1-{2 \over n}\biggr)
\cdots
\biggl(1-{k-1 \over n}\biggr)
=\prod_{i=1}^{k-1} \biggl(1-{i \over n}\biggr)
\] Iz razvoja v Taylorjevo vrsto dobimo \[
e^{-x} = 1-x+ {x^2 \over 2!} - {x^3 \over 3!} + \cdots,
\] Od tod ocenimo \(1-x \approx e^{-x}\) in dobimo \[
\prod_{i=1}^{k-1} \biggl(1-{i \over n}\biggr)
\ \ \approx\ \
\prod_{i=1}^{k-1} e^{-i\over n}\ \ =\ \ e^{-k(k-1)\over 2n}.
\] Torej je verjetnost trčenja \(1\ -\ e^{-k(k-1)/(2n)}\). Potem velja \(e^{-k(k-1)/(2n)} \approx 1-\varepsilon\) oziroma \(-k(k-1)/(2n) \approx \log(1-\varepsilon)\) ali \(k^2-k \approx 2n \log (1-\varepsilon)^{-1}\) in če ignoriramo linearen člen \(-k\), dobimo končno \[
k \approx \sqrt{ 2n \log (1-\varepsilon)^{-1}}.
\] Za \(\varepsilon=0.5\) je \(k \approx 1.17\sqrt{n}\), kar pomeni, da, če zgostimo nekaj več kot \(\sqrt{n}\) elementov, je bolj verjetno, da pride do trčenja kot da ne pride do trčenja.
V splošnem si zapomnimo, da je \(k\) proporcionalen z \(\sqrt{n}\).
Tehniki iskanja trčenja rečemo v kriptografiji napad s paradoksom rojstnih dnevov (angl. Birthday Attack). Le-ta nam določi spodnjo mejo za velikost zaloge vrednosti zgoščevalne funkcije.
Iz zgoraj opisanih lastnosti sledi, da se mora zgoščevalna funkcija razpršiti čim bolj enakomerno po prostoru, ki ga ima na razpolago. Zaradi teh lastnosti imajo zgoščevalne funkcije veliko možnih primerov uporabe. V računalništvu jih najdemo, med drugim, v podatkovnih bazah, podatkovnih strukturah in nenazadnje v računalniških komunikacijah, kjer jih uporabljamo zato, da bi imeli čim bolj varno in zanesljivo komunikacijo, v nadaljevanju pa se bomo omejili samo na ta zadnji primer uporabe.
3.2.2 Zgoščevalne funkcije v računalniških komunikacijah
Ker smo na spletu podvrženi raznim nevarnostim, uporabljamo razne protokole (glej RSA, SSL, DES, …), da bi zagotovili:
Integriteto (ang. integrity): želimo preprečiti možnost, da nekdo spremeni podatke, ki si jih dve osebi izmenjujeta, ne da bi le-ti zaznali spremembe v sporočilu;
Avtentikacijo (ang. authentication): želimo biti zmožni dokazati identiteto svojega sogovornika. Ta lastnost je še posebej pomembna, ko preko spleta pošiljamo osebne podatke;
Onemogočanje zanikanja (ang. non repudiation): želimo dokazati, da je neka oseba res bila tista, ki je poslala določeno sporočilo.
V osnovi so v dobri meri te lastnosti zagotovljene z uporabo zgoščevalnih funkcij in enkripcije čistopisa. Na primer, ko želimo sporočilo m poslati preko interneta: sporočilu dodamo njegovo zgoščeno vrednost H(m), prejemnik sporočila bo prejel sporočilo m’, ki je lahko enako sporočilu, ki smo ga poslali, z druge strani pa se je lahko nekdo vrinil v komunikacijo in spremenil čistopis m ter ga nadomestil z m’. Prejemnik bo izračunal zgoščeno vrednost H(m’) in jo primerjal s H(m), ki je prejel. V primeru, da sta enaki, bo vedel, da med komunikacijo sporočilo m ni bilo spremenjeno. Če nista, bo vedel, da je nekdo sporočilo spremenil. Seveda je dejanski postopek bistveno kompleksnejši, saj v primeru, da napadalec izve za zgoščevalno funkcijo, ki jo sogovornika uporabljata, lahko nadomesti tudi zgoščeno vrednost. Zato, da se to ne bi zgodilo, se poleg čistopisa zgosti še neki tajni podatek, ki ga poznata samo pošiljatelj in prejemnik.
3.2.3 Hashiranje gesel
Drugo področje, kjer uporabljamo zgoščevalne funkcije za zagotavljanje varnosti, je v hranjenju gesel na strežnikih.
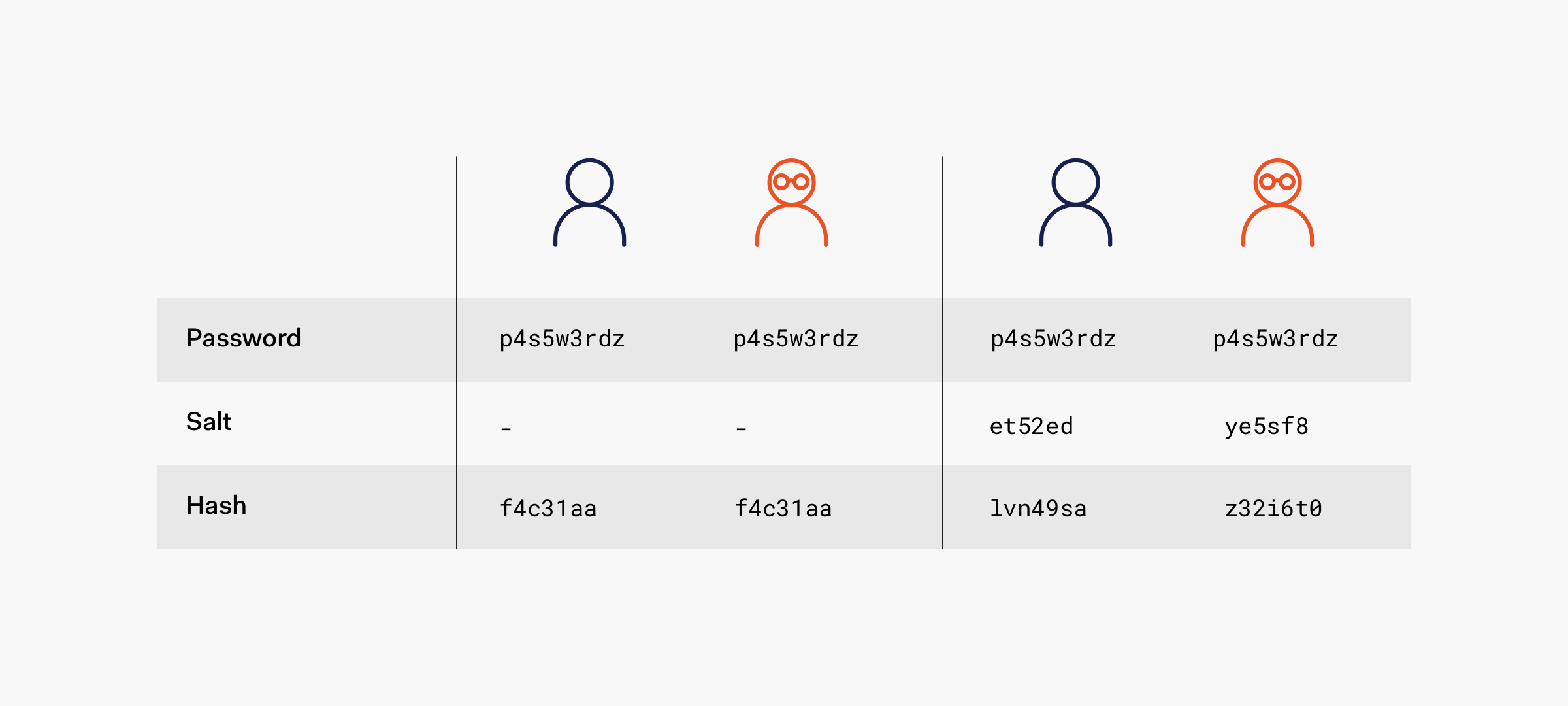
Osnovna ideja je, da v primeru, ko nekdo uspe iz kakršnegakoli razloga dobiti dostop do računalnika, kjer so shranjena gesla, le-ta ne uspe izluščiti gesel uporabnikov. Denimo konkreten primer: Facebook ima več kot dve milijardi uporabnikov. Vsak, ki želi vstopiti v svoj račun, mora dokazati svojo identiteto s tem, da vnese svoj e-mail in neko geslo. E-mail je v večini primerov javen, z druge strani pa je geslo nekaj, kar pozna samo uporabnik. Le-ta seveda hoče, da ostane njegovo geslo tajno (še posebej če uporablja isto geslo za več spletnih strani). Recimo, da bi Facebook hranil gesla v čistopisu (npr. geslo uporabnika je ‘12345’ in je na strežniku geslo shranjeno kot ‘12345’). Ko neki uporabnik želi vstopiti, sistem preveri, ali je vnešeno geslo enako tistemu, ki je hranjeno na strežniku. Tak sistem deluje v redu, dokler napadalec ne uspe vstopiti v računalnik, kjer so hranjena gesla in si tako brez težav prilasti gesla vseh uporabnikov. Seveda se skušamo izogibati takemu sistemu, žal pa je še vedno veliko takih spletnih strežnikov, ki hranijo gesla v čistopisu; nenazadnje nismo zaman omenili takega velikana kot je Facebook: ravno v prvih mesecih leta 2019 smo izvedeli, da je Facebook hranil gesla stotin milijonov uporabnikov v čistopisu, lastniki gesel pa so seveda bili v nevarnosti.
Temu služijo mavrične tabele, ki so vnaprej sestavljene tabele čistopisov in njihovih zgoščenih vrednosti, v odvisnosti od zgoščevalne funkcije. Take tabele izredno pohitrijo brute-force napade. Zaradi takega pristopa je Adobe imel kar nekaj težav leta 2013.
Danes najučinkovitejša strategija je hranjenje gesel z zgoščenimi vrednostmi, ki pa se zgostijo skupaj z naključnim podatkom. To zagotovi, da se bodo ista gesla slikala v različne zgoščene vrednosti.
Ker pa varnosti ni nikoli preveč, se lahko uporablja kombinacija zgornjih pristopov in enkripcije. Tako strategijo uporablja na primer Dropbox.
3.3 Zgoščevalne funkcije v kriptografiji
Upper examples should give you the feeling
- What characterization hash function should have,
- What are some counterexamples of the hash functions in real-world,
- Where in computer science, security and cryptography, hash function becomes useful.
Next, it would be nice to see what are some examples of hash function instatiations in computer science. We will mention just some. For more examples follow the link.