Poglavje 5 Šifre

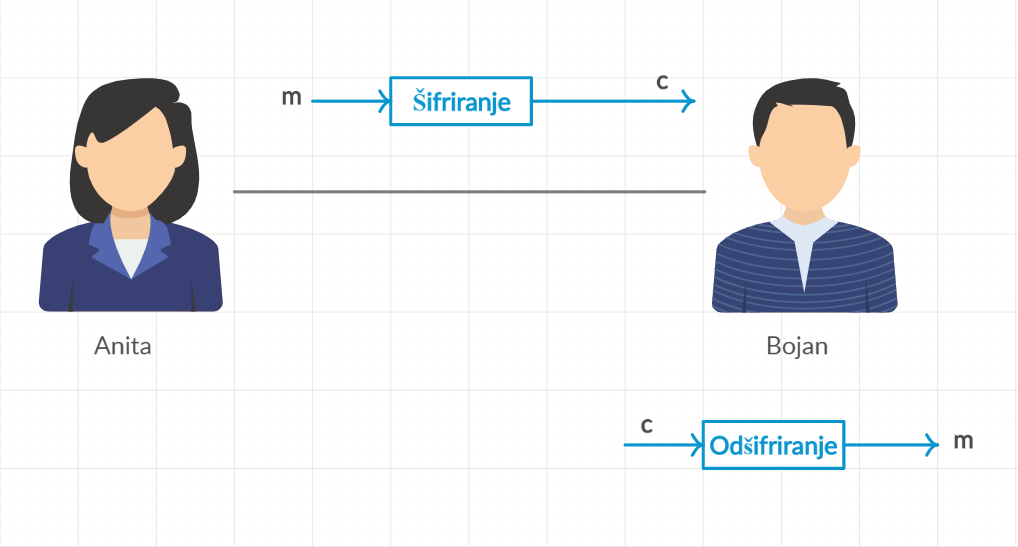
Na sliki ?? je predstavljen osnovni primer komunikacije dveh oseb, Alice in Bob (ki si imata veliko za povedati). Zaradi zaupnosti želita, da njun pogovor ostane skriven. V ta namen uporabljata neke vrste kriptografijo. Pred začetkom morata doreči naslednje stvari:

1. postopek (algoritem), ki bo naredil vsako sporočilo med njima skrivno (tj. šifrirno funkcijo),
2. algoritem za odšifriranje, ki bo omogočil drugi osebi prebrati šifrirano sporočilo (odšifrirna funkcija),
3. množico, iz katere bosta izbirala skrivne ključe (prostor ključev),
4. množici sporočil in šifriranih sporočil, ki jih bosta izmenjevala prek kanala, tj.

1. definicijsko območje šifrirne funkcije,
2. zaloga vrednosti šifrirne funkcije (definicijsko območje odšifrirne funkcije).

Zgornjemu bomo rekli opis kriptosistema.

Postopek, s katerim naredimo sporočilo skrivno, imenujemo šifriranje. Zašifrirano sporočilo imenujemo tajnopis. Postopek, s katerim naredimo sporočilo spet berljivo, imenujemo odšifriranje. Odšifrirano sporočilo je enako začetnemu tekstu, ki ga imenujemo čistopis. Ko je kriptosistem opisan, Alice in Bob lahko začneta pogovor.

0. Kaj se zgodi, ko Alice želi poslati sporočilo Bobu?

Ko Alice želi poslati sporočilo \(m\) Bobu, najprej zašifrira \(m\) v tajnopis \(c\) in ga pošlje Bobu prek kanala (kot to naredi https protokol). Ko Bob prejme \(c\), ga mora najprej odšifrirati, da ga lahko prebere. Tajnopis \(c\) ne sme biti na lahek način povezan s čistopisom \(m\) brez poznavanja ključa, saj nočemo, da bi lahko kdorkoli, ki je povezan s komunikacijskim kanalom, prebral sporočilo.

Primer 1. Opišimo en konkreten simetrični kriptosistem.

1. Kaj bo šifrirna funkcija?

Enc(m, x):
    for each letter in m:
            letter = letter + x;                                            

Povedano drugače, če imamo abecedo a,b,c,…,z,ž, v tabeli a, zašifrira posamično črko s pravilom:

Enc(m, x):
    for each letter in m:
       letter = a[index(a==letter) + x]

2. Kaj bo odšifrirna funkcija?

Dec(c, x):
    for each letter in c:
       letter = a[index(a==letter) - x]

Ta kriptosistem uporablja za šifriranje in odšifriranje sporočil tokovno šifro.

Tokovna šifra šifrira in odšifrira sporočilo črko po črko.
Bločna šifra šifrira in odšifrira sporočilo blok za blokom.
(3) Katera sporočila želita pošiljati? Npr. slovenski tekst (abeceda s 25 črkami, v tem primeru presledke in ločila ne bomo šifrirali).

4. Kako bodo izgledala šifrirana sporočila? Neke čudne besede, sestavljene iz slovenskih črk.

Primer 2. Definirajmo poseben primer zgornjega kriptosistema z določitvijo (skrivnega) parametra x, npr. x = 3.
Preizkusi sam ta postopek oz. uporabi spodnji primer:

Pridevnik simetrična pomeni, da na obeh straneh (šifriranje/odšifriranje) uporabimo enak ključ (oz. bolj splošno, lahko ključ za šifriranje izpeljemo iz ključa za odšifriranje in obratno).

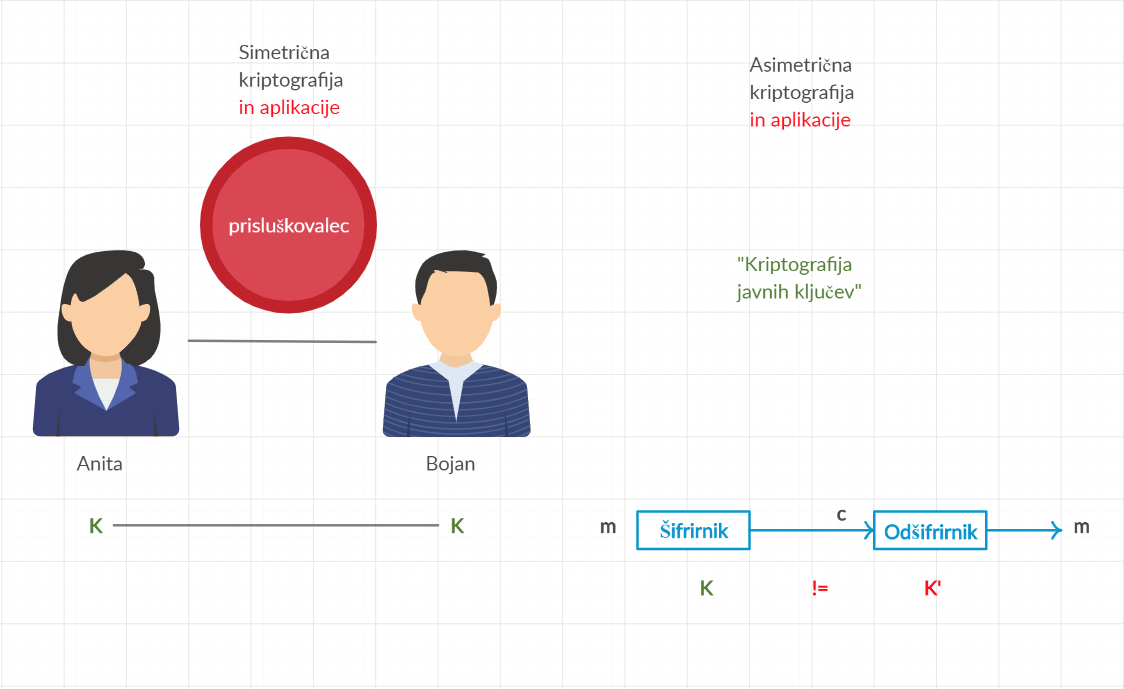
Slika 5.1: Simetrična in asimetrična kriptografija.

Po drugi strani bomo kasneje videli, da asimetrični kriptosistemi namesto skupnega ključa uporabljajo pare ključev (zasebni, javni).

Kriptosistem je algoritem oz. tehnika, ki ohranja skrivnost, omogoča avtentikacijo, celovitost in prepoznavanje nepoštenih ljudi (Stinson and Paterson 2018). Slednji ima za cilj, da ne sporoči več, kot je vidno v šifriranem sporočilu.

Poudarimo, da so kriptosistemi kontrolirani s ključi, ki določijo transformacijo podatkov. Seveda imajo ključi digitalno obliko (binarno zaporedje: 01001101010101…). Za analizo varnosti kriptosistema opazujemo moč napadalca na tem sistemu. Držali se bomo Kerckhoffsovega principa, ki pravi, da

“napadalec” pozna kriptosistem oziroma algoritme,
ki jih uporabljamo, ne pa tudi ključe,
ki nam zagotavljajo varnost.

Močnejši je napadalec, manj varen je kriptosistem.

5.1 Klasične šifre

Pomena informacije se v naši družbi dobro zavedamo - na koncu koncev se veliko posameznikov in podjetij preživlja zgolj z zbiranjem, urejanjem in posredovanjem informacij. Včasih želimo tudi omejiti dostop do informacij in ena izmed možnosti je njihovo šifriranje. Takemu postopku pravimo šifra (angl. cipher), izhaja pa iz hebrejske besede saphar, ki pomeni šteti/označiti. S problemom, kako si osebi (poimenujmo ju Anita in Bojan) izmenjata sporočilo, ne da bi ga opazovalec (Oskar) razvozlal, se (med drugim) ukvarja kriptologija. Ta izraz je sestavljen iz grških besed kryptos, ki pomeni skrivnost, in logos, ki pomeni beseda. Spoznali bomo dva pristopa za reševanje tega problema. V tem poglavju predstavimo zasebne oziroma simetrične šifre, kasneje pa bomo predstavili tudi šifre z javnimi ključi oziroma asimetrične šifre.

Zelo enostaven način za šifriranje besedila so poznali že v rimskih časih, šifrirali so tako, da so zamaknili abecedo za nekaj znakov. Število, ki nam pove, za koliko znakov smo zamaknili abecedo, označimo s \(K\) in predstavlja ključ za šifriranje in odšifriranje sporočila. Če si izberemo \(K=3\), namesto črke A v sporočilu pišemo Č, namesto B črko D in tako naprej do Ž, namesto katerega pišemo črko C. To šifriranje je pogosto uporabljal tudi Julij Cezar in ni preveč varno, saj bi lahko vsakdo v kratkem času kar “na roko” preveril vseh 24 možnosti.

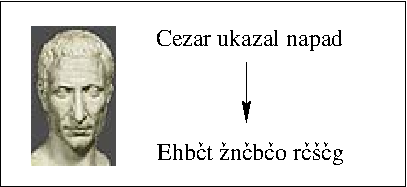
Slika 5.2: Cezarjeva šifra zašifrira njegovo ime v Ehbčt (EHBČT ŽNČBČO RČŠČG)

Najbolj razširjena šifra po drugi svetovni voj-ni je bil DES (Data Encription Standard) in je uporabljal 56-bitne ključe, kar pomeni \(2^{56}\) možnosti za izbiro ključa.

Zaradi vse hitrejših računalnikov so ga leta 2000 nadomestili z AES (Advanced Encription Standard), ki lahko uporablja ključe dolžin 128, 196 in 256 bitov.

(Nekaj navodil: vhod in ključ morata biti hexadecimalna, za male črke (abcdef), da bo okno dovolj veliko. Če je vhoda premalo, se doda padding z ničlami).

DES in AES sta bločni šifri, ker delujeta na blokih (tj. skupini zaporednih znakov). Znake mešata v več krogih z enostavnimi operacijami, katerih vrstnega reda ne moremo spreminjati, ne da bi ostala šifra nespremenjena.
Take operacije so modularna aritmetika, ekskluzivni ali, ciklični zamik, pogled v tabele itd.

Po drugi strani pa lahko za dodatno varnost uporabimo vrstni red blokov. Bločne šifre kot smo jih trenutno opisali enostavno razdelijo sporočilo na bloke zahtevane dolžine, vsakega zašifrirajo in pridobljene tajnopise združijo v istem vrstnem redu. Kriptologi so sčasoma prišli do ideje, da bi na šifriranje enega bloka vplivali tudi drugi bloki. Eden izmed takšnih pristopov, ki se pogosto uporablja je veriženje blokov (Cipher Block Chaining - CBC po angleško). Ideja je, da pred šifriranjem v blok z operacijo ekskluzivni ali primešamo še rezultat prejšnjega šifriranja. Na ta način je tajnopis odvisen od vseh podatkov, ki so prišli pred njim. Delovanje CBC si lahko pogledamo v sledeči aplikaciji.

Podroben opis teh šifer pa žal presega okvire uvoda. Za računske moči napadalcev si oglejte npr. http://crypto-systems.com/, http://keylength.html in http://valjhun.fmf.uni-lj.si/~ajurisic/sc/m3.pdf.

Preden si lahko Anita in Bojan začneta pošiljati sporočila, se morata dogovoriti, na kakšen način bosta šifrirala sporočila, in določiti skrivni ključ \(K\). Bistveno je, da napadalec Oskar ne izve za skrivni ključ, saj bi lahko sicer brez težav prebiral (in ponarejal) sporočila. Načina šifriranja pa običajno ne skrivamo, saj izkušnje kažejo, da ga napadalec slej ko prej odkrije.

Kerckhoffov princip Nasprotnik pozna šifro oziroma algoritme, ki jih uporabljamo, ne pa tudi ključev, ki nam zagotavljajo varnost.

Varnost šifriranja je tako odvisna od zasebnega ključa, za katerega se dogovorita Anita in Bojan. Za tako šifro pravimo, da je zasebna oziroma simetrična, saj imata Anita in Bojan enak zasebni ključ (glej sliko 5.1 ).

Največja nevšečnost takšnega pristopa je torej, da se morata Anita in Bojan pred dopisovanjem sestati. To je za zaljubljen par vsekakor smiselno, v primeru internetnega trgovanja pa nikakor ne. Omenimo še eno pomanjkljivost, ki jo ima takšen način: če povečujemo število posameznikov, ki želijo varno komunicirati v omrežju, narašča tudi število kjučev za vsakega uporabnika. Na sliki 5.2 lahko vidimo primer omrežja z devetnajstimi uporabniki.

Simetrična šifra uporablja isti ključ za šifriranje in odšifriranje.

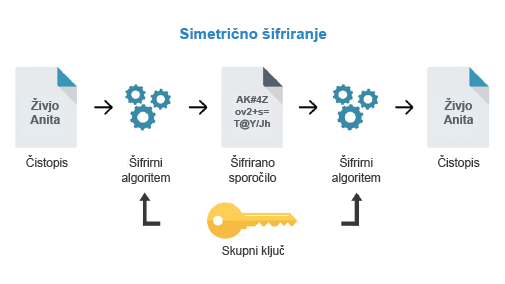
Slika 5.3: Simetrično šifriranje

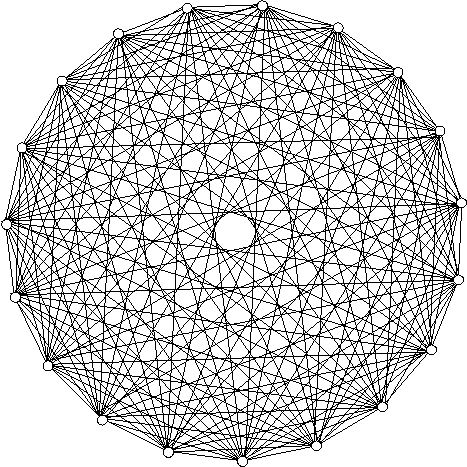
Slika 5.4: Če v kriptosistemu, ki uporablja simetrično šifro, predstavimo uporabnike s točkami, je ključ za vsak par predstavljen z ustrezno povezavo. Že pri devetnajstih uporabnikih postane prostor okrog vsakega uporabnika precej zapolnjen.

Za občutek kakšen problem predstavlja prostor za shranjevanje ključev, si zamislimo, da jih uporabniki shranjujejo na pametnih karticah (mednje štejemo npr. SIM kartice v mobilnih telefonih, zdravstvene kartice \(\ldots\)).

Če imamo na razpolago npr. 8 KB pomnilnika in uporabljamo 128-bitne ključe, lahko na kartico shranimo le 512 ključev. To je odločno premalo že za varno komunikacijo uslužbencev v velikem trgovskem podjetju. Tudi če bi imeli na razpolago večji pomnilnik, pa za potrebe bank, pošt ali zdravstva nikakor ne bi mogli v njem hraniti vseh ključev prebivalcev naše države. V praksi problem pomanjkanja prostora rešimo tako, da uporabnike razdelimo v skupine (glej sliko 5.3 ).
Vsak uporabnik ima svoj ključ in ključe vsake skupine. Vsaka skupina ima ključ za to skupino in t.i. ``glavni’’ ključ (angl. master key), s katerim lahko iz serijske številke uporabnika izračuna uporabnikov ključ. S pomočjo teh ključev se uporabnik in skupina medsebojno overita (tj. preverita pristnost) na način, prikazan na sliki 5.4 .

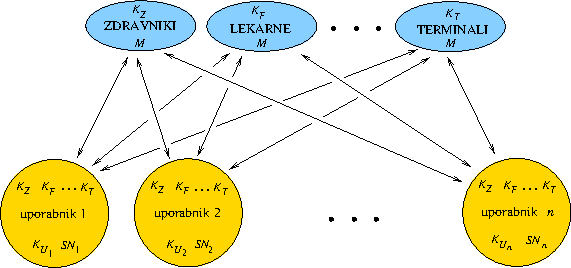
Slika 5.5: Delitev na skupine

Delitev na skupine pri naši zdravstveni kartici. S \(K\) so označeni posamezni ključi, glavni ključ je označen z \(M\). Vsak uporabnik ima tudi enolično serijsko številko \({\tt SN}_i\).

Z \(e_K\) označimo šifrirno funkcijo s ključem \(K\). Le-ta pretvori s ključem \(K\) vsebino v oklepaju v šifrirano besedilo. V zgornjem delu kartica overi terminal s skupinskim ključem \(K_S\) skupine \(S\), v spodnjem delu pa terminal overi pametno kartico z glavnim ključem \(M\) in serijske številke kartice (\({\tt SN}\)). Kartica vsebuje samo \(K_U\) in \(K_S\) ne pa tudi \(M\), medtem ko terminal ne pozna \(K_U\), ampak ga izračuna z \(M\).

Vendar pa imajo vsi kriptosistemi, ki temeljijo na takšni shemi, kar nekaj pomanjkljivosti. Ena izmed večjih je ta, da varnost celotnega sistema temelji na varnosti ene same kartice.

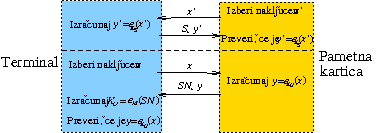
Slika 5.6: Pametna kartica predstavlja uporabnika, terminal pa skupino.

Če namreč uspemo odpreti uporabniško kartico, se dokopljemo do vseh skupinskih ključev. To nam omogoča, da se predstavimo ostalim uporabnikom kot katerakoli skupina, ne da bi uporabnik posumil, da ne komunicira s pravim članom skupine. Če pa se dokopljemo do glavnega ključa, lahko enostavno ponarejamo uporabniške kartice, saj si serijsko številko izmislimo, ustrezen uporabnikov ključ pa nato z glavnim ključem preprosto izračunamo.

Varnost celotnega kriptosistema ne sme biti odvisna od varnosti ene same kartice.

Naslednja pomanjkljivost je ta, da so vse osebe znotraj ene skupine enakovredne, tj. če uporabnik komunicira npr. z lekarno, lahko katerakoli oseba iz skupine lekarn prisluškuje pogovoru. Pa ne samo to, osebe znotraj ene skupine so tudi neločljive, kar pomeni, da se lahko ena oseba iz iste skupine izgovarja, da nečesa ni naredila, čeprav v resnici temu ni tako. Poleg tega je shema povsem neuporabna, če nimamo naravne hierarhične zgradbe, ki nam omogoča delitev na skupine.

Druga rešitev problema s prostorom pa je prikazana na sliki 5.5 , njen najbolj poznan predstavnik pa je Kerberos.

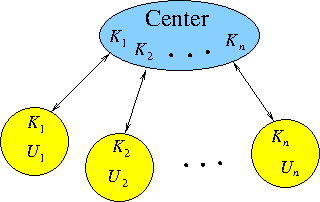
Slika 5.7: Centralna rešitev s simetričnim sistemom.

V tem primeru imamo center, s katerim vsak uporabnik deli svoj skrivni ključ. Ko želi Anita komunicirati z Bojanom, pošlje centru zašifriran zahtevek. Center generira ključ in zašifriranega pošlje Aniti in Bojanu. Bojan nato obvesti Anito, da je prejel ključ in komunikacija se lahko začne. Celoten potek je prikazan na sliki 5.6 .

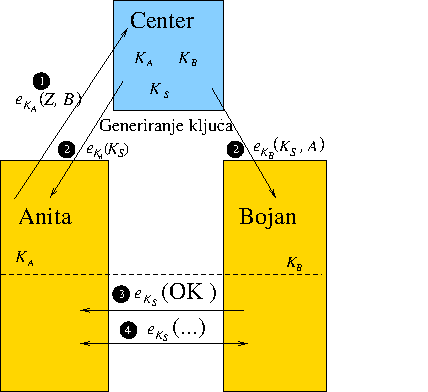
Slika 5.8: Komunikacija

V prvem koraku Anita pošlje centru zašifriran zahtevek za pogovor z Bojanom.

Center nato v drugem koraku generira ključ in ga pošlje obema.

Bojanu tudi sporoči, kdo želi komunicirati z njim.

Bojan v četrtem koraku pošlje sporočilo Aniti, da potrdi sprejetje ključa.

Nato se začne komunikacija.

Očitna pomanjkljivost te sheme je, da moramo vsakič, ko želimo komunicirati, najprej vzpostaviti povezavo s centrom. Pogosto to ni zaželeno ali pa sploh ni možno. Če uporabniški ključi v centru niso primerno zaščiteni, je varnost celotne sheme ogrožena.

Kartic ni potrebno vedno odpirati, da bi prišli do ključev, ki jih hranijo, pač pa je dovolj, da znamo natančno izmeriti porabo energije v času računanja ter uporabiti nekaj statistike.

Zaradi vseh teh pomanjkljivosti se sheme, ki temeljijo na simetričnem pristopu, uporabljajo bodisi v zaprtih okoljih bodisi tam, kjer ni velike potrebe po varnosti. Takšne sheme se na primer uporabljajo za kartice, ki hranijo administrativne podatke, tako da ni potrebno ročno vnašati podatkov v formularje. Naša zdravstvena kartica je tipičen primer take kartice. Za hranjenje občutljivih podatkov pa so takšne sheme primerne le v okoljih, kjer so vsi uporabniki ves čas povezani v mrežo. V primeru naše zdravstvene kartice pa temu ni tako, saj nam sicer ne bi bilo potrebno skoraj vsakič, ko jo želimo uporabiti, iti najprej do terminala, da ji podaljšamo veljavnost.

5.2 Cezarjeva šifra

Kadar želimo podatke zaščititi, da jih ne morejo prebrati tiste osebe, katerim sporočilo ni namenjeno, jih moramo na nek način zaščititi. Eden od postopkov za dosego tega cilja je šifriranje (angl. cipher), izhaja pa iz hebrejske besede saphar, ki pomeni šteti/označiti. S problemom kako zaščititi ta sporočila, da jih ljudje, katerim ta niso namenjena, ne morejo razvozlati, se ukvarja kriptografija. Ta izraz je sestavljen iz grških besed kryptos, ki pomeni skrivnost, in logos, ki pomeni beseda.

Cezarjeva šifra je ena od nastarejših in najpogosteje uporabljenih oblik šifriranja. Poznali so jo že v rimskih časih in ga je med drugimi uporabljal tudi Julij Cezar po komer se ta šifra imenuje. Šifriranje poteka tako, da vsako črko abecede zamaknemo za določeno število znakov. Šifro je zato možno razbiti precej preprosto kajti na voljo je le 24 kombinacij, ki pa jih lahko razbijemo kar “na roke”.

5.2.1 Postopek

Postopek lahko ponazorimo tako, da vsako črko označimo po vrsti s številko od 1 do 25. Nato izberemo, za koliko mest bomo zamaknili naš čistopis. Naše besedilo nato pretvorimo v številke, ki pripadajo posamični črki in tem potem prištejemo zamik. Vsem številkam, ki so večje od 25, odštejemo 25 in nato v tabeli pogledamo, katera številka je katera črka, s čimer pretvorimo besedilo nazaj v črke.

alternativa:

Namesto tabele lahko uporabimo tudi krog črk.

Pri tem najprej ugotovimo, katero črko predstavlja naš zamik. Ta je črka ki je n-ta (zamik + 1) po vrsti vseh črk. Nato A zunanjega kroga z našo n-to črko notranjega kroga. Črke potem eno po eno začnemo prepisovati iz čistopisa v tajnopis, vendar namesto da zapišemo črko samo, jo poiščemo na zunanjem delu kroga in črko, ki se na tem nahaja na notranjem krogu zapišemo v tajnopis.

5.3 Vigenerjeva šifra

Vigenerjeva šifra je različica Cezarjeve šifre, pri kateri za vsako številko uporabimo drugo Cezarjevo šifro, ki jo določa geslo. Šifra je bila prvič zabeležena leta 1553 v knjigi Giovana Battista Bellasa ampak je bila v 19. stoletju napačno pripisana Blaiseju de Vigenèrju, od koder je tudi dobila svoje ime. Šifra je bila izredno preprosta za implementacijo in pojasnilo, vendar je učenjaki niso uspeli razbiti več kot 300 let, ko je Friedrich Kasiski uspel razviti splošno metodo za razbijanje. Zaradi tega razloga se jo je v tem času prijelo ime le chiffre indéchiffrable (francosko za šifra, ki se je ne da razbiti).

5.3.1 Postopek

Ponovno bomo uporabili tabelo, ki smo jo uporabili pri Cezarjevi šifri. Prvi korak je, da pretvorimo posamične črke gesla v številke in nato od vsake odštejemo 1. Nato ta postopek naredimo še z našim čistopisom. Prvo številko čistopisa seštejemo s prvo številko iz gesla, drugo čistopisa z drugo gesla in tako naprej. Ko nam zmanjka gesla začnemo geslo ponovno s prvo številko medtem ko čistopis nadaljujemo eno črko za drugo. Ko pridemo do konca vsem številkam večjim od 25 odštejemo 25 in nato vsako številko poiščemo v tabeli ter jih po vrsti zabeležimo, kar nam predstavlja tajnopis.

alternativa

Za ta postopek šifriranja lahko uporabimo tudi krog črk, ki smo ga uporabili pri Cezarjevi šifri, kar naredi ta postopek še lažji. Na zunanjem krogu A poravnamo s prvo črko gesla. Nato na zunanjem krogu poiščemo prvo črko čistopisa. Črka, ki se nahaja pod njo predstavlja prvo črko tajnopisa. To naredimo za vsako črko. Če nam med tem zmanjka gesla preprosto pričnemo z njim od začetka.

5.3.2 Vigenerjeva šifra z krogom

5.3.3 Vigenerjeva šifra brez kroga

5.3.4 Napad na Vigenerjevo šifro

5.4 Afina šifra

5.4.1 Postopek

Postopek lahko ponazorimo tako, da vsako črko označimo po vrsti, s številko od 1 do 25. Linearnim funkcijam, definiranim s ključem, izberemo, za koliko mest bomo zamaknili naš čistopis. Naše besedilo nato pretvorimo v številke, ki pripadajo posamični črki in tem potem prištejemo zamik. Vsem številkam, ki so višje od 25 odštejemo 25 in nato v tabeli pogledamo, katera številka je katera črka, s čimer pretvorimo besedilo nazaj v črke.

Vhod naj bodo štirije tekstovni vhodi oz. izhodi:

• Vhodna abeceda (poljubni različni znaki (UTF-8)).
• Ključ za enkripcijo \((a,b)\) - dva vhoda.
• Vhodni čistopis \(P\).

Šifriranje oz. odšifriranje s ključem \((a,b)\):

• Šifriramo vsako črko posebej.
• \(E_{(a,b)}(x) = a x + b \mod n\), kjer je \(x\) indeks črke v abecedi in \(n\) dolžina abecede.
• Odšifriranje je v obratnem vrstnem redu šifriranja \(D_{(a,b)}(x) = a^{-1} (x - b) \mod n\).

Izhod naj bo tajnopis in tabela, ki definira preslikavo.

• Tajnopis, kot tekstovni izhod.
• Šifrirna tabela.

Namigi in dodatne ideje:

• Za dešifriranje lahko uporabimo isto shemo. Potrebno je preračunati kjuč \((a, b) \mapsto (a^{-1}, -a^{-1}b)\) (lahko uporabiš REA za izračun obratnega elementa v \(\mathbb{Z}_n\)).
• V primeru, da uporabnik uporabi napačen kjuč (šifriranje ni bijekcija), ga interakcija opozori (ponudi mu možne izbire za \(a\) - števila, ki so tuja z \(n\)), ampak pripadajočo tabelo še vedno izpiši.

• Za smiselno funkcioniranje imamo gumbe s pripadajočimi akcijami:

• Gumb, ki samo izpiše šifrirno oz. odšifrirno tabelo.
• Gumb, ki izračuna, kjuč za odšifriranje

• Gumb, ki šifrira oz. odšifrira besedilo.

5.5 Pretvornik med abecedami

Začnite pisati na enem od polj. S klikom na gumb za vnos, bo pretvorba opravljena. V primeru težav nas kontaktirajte s spodnjim obrazcem.

5.5.1 Učenje novih adeced

Po opazovanju primera pretvorbe med slovensko gajico in srbsko cilirico, in slovensko gajico in rusko cilirico, in slovensko gajico in glagolico, poskusite, koliko ste se naučili.