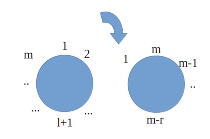
Kot lahko vidite, ko ste 11-krat premešali kupca sta vrhnji karti enaki
Za obrazložitev trika bomo rešili naslednje tri enačbe z uporabo KIO.
Uporabite lahko online pripomočke za razreševanje takih enačb, lahko pa poskusite sami
(
\(x \equiv -1 \pmod 4 \)
\(x \equiv -1 \pmod 3 \)
\(x \equiv -1 \pmod 2 \)